Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2;0;0), D(0;3;0), S(0;0;4) (hình 19) a) Tìm tọa độ điểm C b) Viết phương trình mặt phẳng (SBD) c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD)
Đề bài
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2;0;0), D(0;3;0), S(0;0;4) (hình 19)
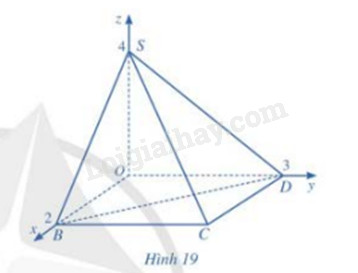
a) Tìm tọa độ điểm C
b) Viết phương trình mặt phẳng (SBD)
c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD)
Phương pháp giải - Xem chi tiết
a) Quan sát hình vẽ
b) Tìm cặp vecto chỉ phương của mặt phẳng để tìm vecto pháp tuyến. Sử dụng phương trình tổng quát của mặt phẳng
c) M(a;b;c), (P): Ax + By + Cz + D = 0. Ta có: \(d(M;(P)) = \frac{{\left| {A.a + B.b + C.c + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Lời giải chi tiết
a) C(2;3;0)
b) \(\overrightarrow {SB} = (2;0; - 4);\overrightarrow {SD} = (0;3; - 4)\)
Vecto pháp tuyến của mặt phẳng (SBD) là: \(\overrightarrow n = \left[ {\overrightarrow {SB} ;\overrightarrow {SD} } \right] = (12;8;6) = 2(6;4;3)\)
Phương trình mặt phẳng (SBD) là: \(6x + 4y + 3z - 12 = 0\)
c) \(d(C;(SBD)) = \frac{{\left| {6.2 + 3.( - 4) - 12} \right|}}{{\sqrt {{6^2} + {4^2} + {3^2}} }} = \frac{{12\sqrt {61} }}{{61}}\)