Giải bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều
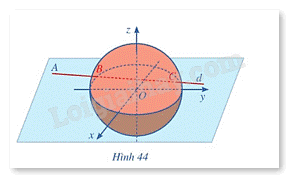
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {91;75;0} \right)\) hướng về đài kiểm soát không lưu (Hình 44).
Đề bài
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {91;75;0} \right)\) hướng về đài kiểm soát không lưu ( Hình 44 ).
a) Xác định toạ độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
b) Xác định toạ độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.
c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.
Phương pháp giải - Xem chi tiết
a) + Viết phương trình đường thẳng d đi qua điểm A và có một vectơ chỉ phương \(\overrightarrow u \).
+ Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa. B thuộc d nên tính tọa độ của B theo t.
+ B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\). Từ đó có phương trình theo ẩn t, giải phương trình tính t.
+ Thay giá trị t tính được để tìm tọa độ B, so sánh giá trị và được ra kết luận.
b) + Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất.
+ Vì H thuộc d nên tính tọa độ của H theo t’.
+ OH ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\), từ đó tính được t’.
+ Từ đó tính được H và khoảng cách OH cần tìm.
Lời giải chi tiết
a) Đường thẳng d đi qua điểm A(-688;-185;8), có một vectơ chỉ phương \(\overrightarrow u = \left( {91;75;0} \right)\) có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 688 + 91t\\y = - 185 + 75t\\z = 8\end{array} \right.\) (t là tham số).
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì B thuộc d nên B(-688+91t; -185+75t;8).
Để B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\).
Do đó, \(\sqrt {{{\left( { - 688 + 91t} \right)}^2} + {{\left( { - 185 + 75t} \right)}^2} + {8^2}} = 417\)
\( \Leftrightarrow 13\;906{t^2} - 152\;966t + 333\;744 = 0\)\( \Leftrightarrow t = 3\) hoặc \(t = 8\)
Với \(t = 3\) ta có B(-415; 40; 8) và \(AB = \sqrt {{{\left( { - 415 + 688} \right)}^2} + {{\left( {40 + 185} \right)}^2}} = \sqrt {125\;154} \)
Với \(t = 8\) ta có B(40; 415; 8) và \(AB = \sqrt {{{\left( {40 + 688} \right)}^2} + {{\left( {415 + 185} \right)}^2}} = \sqrt {889\;984} \)
Vì \(\sqrt {125\;154} < \sqrt {889\;984} \) nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là (-415; 40; 8).
b) Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất. Vì H thuộc d nên H(-688+91t’; -185+75t’;8).
Để OH là ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\)
\( \Leftrightarrow \left( { - 688 + 91t'} \right).91 + \left( { - 185 + 75t'} \right).75 + 8.0 = 0 \Leftrightarrow 13\;906t' - 76\;483 = 0 \Leftrightarrow t' = \frac{{11}}{2}\)
Do đó, \(H\left( {\frac{{ - 375}}{2};\frac{{455}}{2};8} \right)\).
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
\(OH = \sqrt {{{\left( {\frac{{ - 375}}{2}} \right)}^2} + {{\left( {\frac{{455}}{2}} \right)}^2} + {8^2}} = \frac{{\sqrt {347\;906} }}{2}\left( {km} \right)\)
c) Theo a ta có: tọa độ của vị trí mà máy bay ra khỏi màn hình ra đa là: (40; 415; 8).