Giải bài tập 3 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
Đề bài
Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
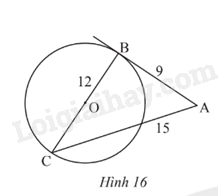
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {CBA} = {90^o}\) hay \(AB \bot BO\) suy ra AB là tiếp tuyến.
Lời giải chi tiết
Theo hình ta có: AB = 9; BC = 12; AC = 15
Suy ra BC 2 = AB 2 + AC 2 nên tam giác ABC vuông tại B
Hay \(\widehat {CBA} = {90^o}\) suy ra \(AB \bot BC\)
Mà \(O \in BC\) nên \(AB \bot BO\)
Vậy AB đi qua B (B \( \in (O)\)) và \(AB \bot BO = R\) nên AB là tiếp tuyến của đường tròn (O).
Cùng chủ đề:
Giải bài tập 3 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo