Giải bài tập 4. 18 trang 89 SGK Toán 9 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.

Trong Hình 4.32, mặt tiền mái nhà có chiều rộng $BC = 3m$ và hai bên mái AB, AC cùng bằng 1,8m.

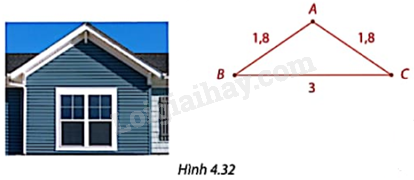
a) Tính chiều cao AH của mái nhà.

b) Tính góc BAC tạo bởi hai mép của mái nhà.

Lời giải chi tiết

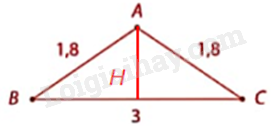
a) Tam giác ABC cân tại A nên AH là đường cao đồng thời là đường trung tuyến nên $BH = HC = \frac{{BC}}{2} = \frac{3}{2} = 1,5m$.

Tam giác ABH vuông tại H nên

$A{H^2} + B{H^2} = A{B^2}$ (định lí Pythagore)

Do đó, $AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {1,{8^2} - 1,{5^2}}  = \frac{{3\sqrt {11} }}{{10}} \approx 1\left( m \right)$

b) Tam giác BHA vuông tại H nên

$\sin BAH = \frac{{BH}}{{AB}} = \frac{{1,5}}{{1,8}} = \frac{5}{6}$, suy ra $\widehat {BAH} \approx {56^o}27'$.

Tam giác ABC cân tại A nên AH là đường cao đồng thời là đường phân giác của tam giác.

Do đó, $\widehat {BAC} = 2\widehat {BAH} \approx {112^o}54'$