Giải bài tập 5.15 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K; b) KH < BC.
Đề bài
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Phương pháp giải - Xem chi tiết
Trong đường tròn, đường kính là dây lớn nhất
Tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
Lời giải chi tiết
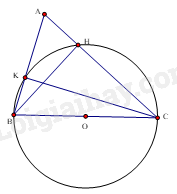
a) Gọi trung điểm của BC là O
Tam giác vuông BKC có KO là đường trung tuyến KO ứng với cạnh huyền BC nên KO = OB = OC hay B, K, C thuộc đường tròn tâm O đường kính BC (1)
Tam giác BHC vuông tại H có HO là đường trung tuyến ứng với cạnh huyền BC nên HO = BO = OB hay B, H, C thuộc được đường tròn tâm O đường kính BC (1)
Từ (1) và (2) ta có K, H thuộc đường tròn tâm O đường kính BC.
b) Đường tròn tâm O có BC là đường kính, KH là dây không qua tâm O nên KH < BC.