Giải bài tập 5.35 trang 127 SGK Toán 9 tập 1 - Cùng khám phá
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn với \(MO = 2R\), vẽ hai tiếp tuyến tiếp xúc (O) tại A và B. Viết công thức tính phần diện tích nằm ngoài đường tròn (O) của tứ giác MAOB theo R.
Đề bài
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn với \(MO = 2R\), vẽ hai tiếp tuyến tiếp xúc (O) tại A và B. Viết công thức tính phần diện tích nằm ngoài đường tròn (O) của tứ giác MAOB theo R.
Phương pháp giải - Xem chi tiết
+ Tính số đo góc AOM, từ đó tính được góc AOB, từ đó tính được số đo cung nhỏ AB.
+ Chứng minh \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\), suy ra \({S_{\Delta OAM}} = {S_{\Delta OBM}}\) nên \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}}\).
+ Diện tích hình quạt tâm O, cung nhỏ AB là: ${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{{{360}^{o}}}$.
+ Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q}\).
Lời giải chi tiết
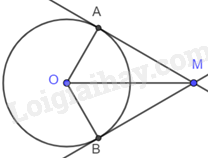
Vì MA, MB là tiếp tuyến của (O) nên
+ \(MA = MB\).
+ OA là tia phân giác của góc AOB, suy ra \(\widehat {AOM} = \widehat {MOB} = \frac{1}{2}\widehat {AOB}\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên \(\Delta AOM\) vuông tại A. Suy ra:
+ \(AM = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = \sqrt 3 R\).
+ \(\cos AOM = \frac{{OA}}{{OM}} = \frac{R}{{2R}} = \frac{1}{2}\) nên \(\widehat {AOM} = {60^o}\), suy ra \(\widehat {AOB} = {2.60^o} = {120^o}\).
Vì AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng 120 độ.
Vì tam giác AOM vuông tại A nên
\({S_{AOM}} = \frac{1}{2}OA.AM = \frac{1}{2}.R.R\sqrt 3 = \frac{{{R^2}\sqrt 3 }}{3}\).
Tam giác OAM và tam giác OBM có:
\(OA = OB\) (= bán kính (O)),
\(OM\) chung,
\(\widehat {AOM} = \widehat {MOB}\left( {cmt} \right)\)
Do đó, \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\).
Suy ra, \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}} = \frac{{2{R^2}\sqrt 3 }}{3}\).
Diện tích hình quạt tâm O, cung nhỏ AB là:
${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{360}=\frac{\pi .{{R}^{2}}.120}{360}=\frac{\pi .{{R}^{2}}}{3}$.
Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q} = \frac{{2{R^2}\sqrt 3 }}{3} - \frac{{\pi .{R^2}}}{3} = \frac{{{R^2}}}{3}\left( {2\sqrt 3 - \pi } \right)\).