Giải bài tập 5.39 trang 113 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác vuông ABC (A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng: a) BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA). b) CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Đề bài
Cho tam giác vuông ABC (A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng:
a) BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta {\rm{ABC}} = \Delta {\rm{A'BC}}\) từ đó suy ra \(\widehat {{\rm{BA'C}}} = \widehat {{\rm{BAC}}} = 90^\circ \).
Do đó BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) Lần lượt chứng minh CA và CA’ là các tiếp tuyến của (B; BA).
Lời giải chi tiết
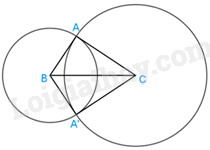
a) Xét tam giác ABC và tam giác A’BC có:
BA = BA’
BC chung
CA = CA’
Suy ra: \(\Delta {\rm{ABC}} = \Delta {\rm{A'BC}}\)(c.c.c)
Do đó: \(\widehat {{\rm{BA'C}}} = \widehat {{\rm{BAC}}} = 90^\circ \) (hai góc tương ứng)
Suy ra: \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên BA’ là tiếp tuyến của (C; CA)
Lại có: \({\rm{CA}} \bot {\rm{BA}}\) tại A nên BA là tiếp tuyến của (C; CA)
Vậy BA và BA’ là hai tiếp tuyến cắt nhau của (B; BA).
b) \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên CA’ là tiếp tuyến của (B; BA)
\({\rm{CA}} \bot {\rm{BA}}\) tại A nên CA là tiếp tuyến của (B; BA)
Vậy CA và CA’ là hai tiếp tuyến cắt nhau của (C; CA).