Giải bài tập 5.7 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng (100^circ )(làm tròn kết quả đến hàng phần mười).
Đề bài
Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng \(100^\circ \)(làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Theo bài 5.6, \(\widehat {HOA} = \frac{{\widehat {AOB}}}{2} = \frac{{100^\circ }}{2} = 50^\circ \). Xét tam giác OAH vuông tại H từ đó tính được độ dài bán kính OA.
Lời giải chi tiết
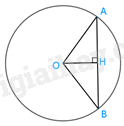
Theo bài ra ta có sđ\(\overset\frown{AB}=100^\circ \).
Kẻ OH là đường cao của tam giác OAB, H \(\in\) AB.
Tam giác OAB cân tại O nên OH đồng thời là đường phân giác, khi đó:
\(\widehat {HOA} = \widehat {HOB} = \frac{{\widehat {AOB}}}{2}\) mà \(\widehat {AOB} = \)sđ\(\overset\frown{AB}=100{}^\circ \)
nên \(\widehat {HOA} = \frac{{100^\circ }}{2} = 50^\circ \)
Xét tam giác OAH vuông tại H có:
\(\cos \widehat {HOA} = \frac{{OH}}{{OA}} \Rightarrow OA = \frac{{OH}}{{\cos \widehat {HOA}}} = \frac{3}{{\cos 50^\circ }} \approx 4,7\)(cm)