Giải bài tập 8 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
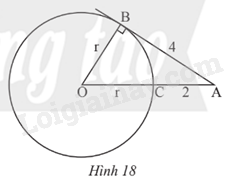
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B. a) Tính bán kính r của đường tròn (O). b) Tính chiều dài cạnh OA của tam giác ABO.
Đề bài
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.
a) Tính bán kính r của đường tròn (O).
b) Tính chiều dài cạnh OA của tam giác ABO.
Phương pháp giải - Xem chi tiết
- Áp dụng định lý Pythagore trong tam giác vuông OAB ta có hệ thức theo r rồi tính r.
- Thay r từ đó ta tính cạnh OA.
Lời giải chi tiết
a) Ta có AB là tiếp tuyến của đường tròn (O) tại B. Do đó \(AB \bot OB\).
Ta có: OA = OC + CA = r + 2
Xét tam giác OAB vuông tại B, ta có:
OA 2 = OB 2 + AB 2 (Áp dụng định lý Pythagore)
Suy ra \({(r + 2)^2} = {r^2} + {4^2}\)
\({r^2} + 4r + 4 = {r^2} + 16\)
4r = 12
r = 3 .
b) Xét tam giác OAB vuông tại B, ta có:
OA 2 = OB 2 + AB 2 = 3 2 + 4 2 = 5 2 .
Suy ra OA = 5.