Giải bài tập 9.10 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng (widehat {EIF} + widehat {BAC} = {180^o})
Đề bài
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat {EIF} + \widehat {BAC} = {180^o}\)
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {IFA} = \widehat {AEI} = {90^o}\)
+ Sử dụng tổng các góc trong tứ giác AEIF tính được tổng \(\widehat {EIF} + \widehat {BAC} = {180^o}\).
Lời giải chi tiết
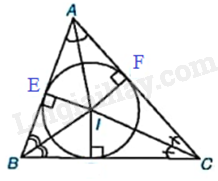
Vì đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F nên \(IF \bot AC,IE \bot AB \Rightarrow \widehat {IFA} = \widehat {AEI} = {90^o}\).
Tứ giác AEIF có:
\(\widehat {EAF} + \widehat {EIF} + \widehat {IFA} + \widehat {AEI} = {360^o}\)
\(\widehat {EIF} + \widehat {EAF} = {360^o} - \left( {\widehat {IFA} + \widehat {AEI}} \right) = {180^o} \)
Vậy \(\widehat {EIF} + \widehat {BAC} = {180^o}\).