Giải câu hỏi trắc nghiệm trang 122 vở thực hành Toán 9
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết (OA = sqrt {15} cm) và (OB = 4cm). Khi đó: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm ngoài (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm trong (O), điểm B nằm trên (O).
Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trả lời Câu 1 trang 122 Vở thực hành Toán 9
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết \(OA = \sqrt {15} cm\) và \(OB = 4cm\). Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Phương pháp giải:
+ Điểm M nằm trên đường tròn (O; R) nếu \(OM = R\).
+ Điểm M nằm trong đường tròn (O; R) nếu \(OM < R\).
+ Điểm M nằm ngoài đường tròn (O; R) nếu \(OM > R\).
Lời giải chi tiết:
Vì \(OA < 4cm\) nên điểm A nằm trong (O) và \(OB = 4cm\) nên điểm B nằm trên (O).
Chọn D
Câu 2
Trả lời Câu 2 trang 122 Vở thực hành Toán 9
Cho Hình 5.42, trong đó BD là đường kính, \(\widehat {AOB} = {40^o};\widehat {BOC} = {100^o}\). Khi đó:
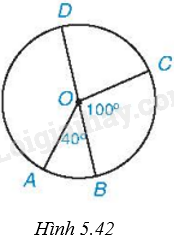
A. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
B. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
C. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
D. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
Phương pháp giải:
Trong một đường tròn, số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó.
Lời giải chi tiết:
Ta có: \(\widehat {BOC} + \widehat {DOC} = {180^o}\) nên \(\widehat {DOC} = {180^o} - \widehat {BOC} = {180^o} - {100^o} = {80^o}\).
\(\widehat {BOA} + \widehat {DOA} = {180^o}\) nên \(\widehat {DOA} = {180^o} - \widehat {BOA} = {180^o} - {40^o} = {140^o}\).
Vì góc ở tâm DOA chắn cung nhỏ AD nên \(sđ\overset\frown{AD}=\widehat{DOA}={{140}^{o}}\).
Vì góc ở tâm DOC chắn cung nhỏ DC nên \(sđ\overset\frown{DC}=\widehat{DOC}={{80}^{o}}\).
Chọn D
Câu 3
Trả lời Câu 3 trang 122 Vở thực hành Toán 9
Cho hai đường tròn \(\left( {A;{R_1}} \right),\left( {B;{R_2}} \right)\), trong đó \({R_2} < {R_1}\). Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.43). Khi đó:
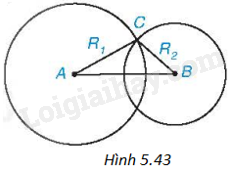
A. \(AB < {R_1} - {R_2}\).
B. \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
C. \(AB > {R_1} + {R_2}\).
D. \(AB = {R_1} + {R_2}\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) (với \(R > r\)) cắt nhau khi \(R - r < OO' < R + r\).
Lời giải chi tiết:
Vì hai đường tròn (A) và (B) cắt nhau nên \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
Chọn B
Câu 4
Trả lời Câu 4 trang 122 Vở thực hành Toán 9
Cho đường tròn (O; R) và hai đường thẳng \({a_1}\) và \({a_2}\). Gọi \({d_1},{d_2}\) lần lượt là khoảng cách từ điểm O đến \({a_1}\) và \({a_2}\). Biết rằng (O) cắt \({a_1}\) và tiếp xúc với \({a_2}\) (H.5.44). Khi đó:
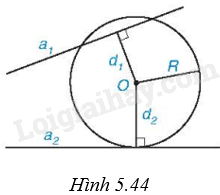
A. \({d_1} < R\) và \({d_2} = R\).
B. \({d_1} = R\) và \({d_2} < R\).
C. \({d_1} > R\) và \({d_2} = R\).
D. \({d_1} < R\) và \({d_2} < R\).
Phương pháp giải:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết:
Vì (O) cắt \({a_1}\) nên \({d_1} < R\). Vì (O) tiếp xúc với \({a_2}\) nên \({d_2} = R\).
Chọn A