Giải câu hỏi trắc nghiệm trang 72, 73 vở thực hành Toán 8
Chọn phương án đúng trong mỗi câu sau:
Câu 1 trang 72
Mỗi tam giác có bao nhiêu đường trung bình?
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp giải:
Dựa vào khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Lời giải chi tiết:
Tam giác có 3 cạnh nên tạo được 3 đường trung bình.
=> Chọn đáp án B.
Câu 2 trang 72
Tìm độ dài x trong Hình 4.10.
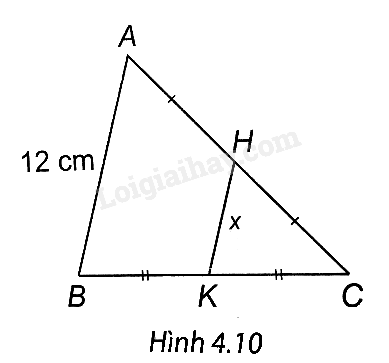
A. 12 cm.
B. 24 cm.
C. 6 cm.
D. 10 cm.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Ta có: H là trung điểm AC, K là trung điểm BC nên HK là đường trung bình của tam giác ABC.
Suy ra, HK // AB. Áp dụng định lí Thales, ta có \(\frac{{HK}}{{AB}} = \frac{{CH}}{{AC}} = \frac{1}{2}\)
Do đó \(HK = \frac{{AC}}{2} = \frac{{12}}{2} = 6\) (cm).
=> Chọn đáp án C.
Câu 3 trang 73
Quan sát Hình 4.11 và chọn khảng định đúng.
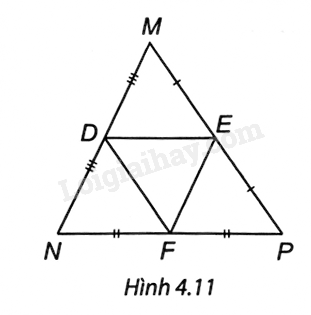
A. DE = NP.
B. DF = 2MP.
C. EF = 2DM.
D. NP = 2DE.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Ta có D là trung điểm MN, E là trung điểm MP, F là trung điểm NP nên DE, EF, DF đều là đường trung bình của tam giác MNP.
Do đó DE // NP, EF // MN, DF // MP và MN = 2EF, NP = 2DE, MP = 2DF.
=> Chọn đáp án D.
Câu 4 trang 73
Cho tam giác ABC có chu vi bằng 20 cm. Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Chu vi tam giác MNP bằng:
A. 20 cm.
B. 10 cm 2 .
C. 10 cm.
D. 40 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tam giác bằng tổng ba cạnh của tam giác đó.
Lời giải chi tiết:
Ta có M, N, P lần lượt là trung điểm của AB, BC, AC nên MN, NP, MP đều là đường trung bình của tam giác ABC.
Khi đó BC = 2MP, AB = 2NP, AC = 2MN
Do đó AB + BC + AC = 2(MN + NP + MP)
Vậy MN + NP + MP = 10 (cm).
=> Chọn đáp án C.
Câu 5 trang 73
Cho ∆ABC đều, cạnh 3 cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng:
A. 8 cm.
B. 7,5 cm.
C. 6 cm.
D. 7 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tứ giác bằng tổng bốn cạnh của tứ giác đó.
Lời giải chi tiết:
Ta có M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên BC = 2MN.
Khi đó MN = 1,5 cm.
Chu vi của tứ giác MNCB là:
MN + NC + BC + MB = 1,5 + 1,5 + 3 + 1,5 = 7,5 (cm).
=> Chọn đáp án B.