Đề thi kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Nam Từ Liêm
Giải chi tiết đề thi kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Nam Từ Liêm với cách giải nhanh và chú ý quan trọng
Bài I (2 điểm) :
1. Tính :
\(a) \;\dfrac{5}{{\sqrt 5 - 1}} - \dfrac{5}{{\sqrt 5 + 1}};\) \( b) \;\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt {\dfrac{1}{5}} \)
2) Giải các phương trình sau :
\(a) \,\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12;\) \(b) \;\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\)
Bài II (2 điểm)
Cho hai biểu thức : \(A = \dfrac{{x + 7}}{{3\sqrt x }}\) và \(B = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x + 1}}{{\sqrt x - 3}} + \dfrac{{7\sqrt x + x}}{{9 - x}}\) với \(x > 0;x \ne 9\)
a) Tính \(A\) khi \(x = 25.\)
b) Chứng minh : \(B = \dfrac{{3\sqrt x }}{{\sqrt x + 3}}.\)
c) Tìm giá trị nhỏ nhất của biểu thức \(P = A.B.\)
Bài III (2 điểm) : Cho đường thẳng \(\left( {{d_1}} \right):y = 2x + 2.\)
a) Vẽ đường thẳng \(\left( {{d_1}} \right)\) trên mặt phẳng tọa độ \(Oxy.\)
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right):y = x - 3.\)
c) Cho đường thẳng \(\left( {{d_3}} \right):y = mx + 5.\) Tìm giá trị của \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\,\left( {{d_2}} \right),\,\left( {{d_3}} \right)\) cắt nhau tại một điểm.
Bài IV (3,5 điểm) :
1. Một con thuyền ở địa điểm \(D\) di chuyển từ bờ sông \(a\) sang bờ sông \(b\) với vận tốc trung bình là \(2km/h,\) vượt qua khúc sông nước chảy mạnh trong \(20\) phút. Biết đường đi con thuyền là \(DE\), tạo với bờ sông một góc bằng \(60^\circ .\) Tính chiều rộng khúc sông.
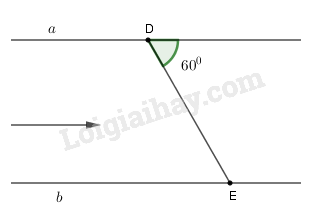
2. Lấy điểm \(A\) trên \(\left( {O;R} \right),\) vẽ tiếp tuyến \(Ax.\) Trên \(Ax\) lấy điểm \(B,\) trên \(\left( {O;R} \right)\) lấy điểm \(C\) sao cho \(BC = AB.\)
a) Chứng minh rằng : \(CB\) là tiếp tuyến của \(\left( O \right).\)
b) Vẽ đường kính \(AD\) của \(\left( O \right),\) kẻ \(CK\) vuông góc với \(AD.\)
Chứng minh rằng : \(CD//OB\) và \(BC.DC = CK.OB.\)
c) Lấy \(M\) trên cung nhỏ \(AC\) của \(\left( O \right),\) vẽ tiếp tuyến tại \(M\)cắt \(AB,\,BC\) lần lượt tại \(E,\,\,F.\) Vẽ đường tròn tâm \(I\) nội tiếp tam giác \(BFE.\) Chứng minh rằng : \(\Delta MAC \backsim \Delta \,IFE.\)
Bài V (0,5 điểm) : Cho \(x,y,z > 0\) và \(xy + yz + xz = 3xyz.\) Tính giá trị nhỏ nhất của :
\(A = \dfrac{{{x^2}}}{{z\left( {{z^2} + {x^2}} \right)}} + \dfrac{{{y^2}}}{{x\left( {{x^2} + {y^2}} \right)}} + \dfrac{{{z^2}}}{{y\left( {{y^2} + {z^2}} \right)}}\)
----------HẾT----------
HƯỚNG DẪN GIẢI CHI TIẾT
Bài I (VD):
Phương pháp:
1) a) Quy đồng mẫu số và rút gọn biểu thức.
b) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}} = \left[ \begin{array}{l}A\,\,\,\,khi\,\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,\,A < 0\end{array} \right.\) và \(\sqrt {\dfrac{1}{A}} = \dfrac{{\sqrt A }}{A}\,\,\left( {A > 0} \right)\)
2) a) Biến đổi đưa về giải phương trình: \(\sqrt A = B\left( {A \ge 0;B \ge 0} \right) \Leftrightarrow A = {B^2}\)
b) Giải phương trình: \(\sqrt A = \sqrt B \,\,\,\left( {A \ge 0;\,\,\,B \ge 0} \right) \Leftrightarrow A = B\)
Cách giải:
1.Tính:
\(\begin{array}{l}a)\,\dfrac{5}{{\sqrt 5 - 1}} - \dfrac{5}{{\sqrt 5 + 1}} = \dfrac{{5\left( {\sqrt 5 + 1} \right) - 5\left( {\sqrt 5 - 1} \right)}}{{\left( {\sqrt 5 + 1} \right)\left( {\sqrt 5 - 1} \right)}}\\ = \dfrac{{5\sqrt 5 + 5 - 5\sqrt 5 + 5}}{{5 - 1}} = \dfrac{{10}}{4} = \dfrac{5}{2}\end{array}\)
\(\begin{array}{l}b)\,\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt {\dfrac{1}{5}} = \left| {\sqrt 5 - 3} \right| - \dfrac{{\sqrt 5 }}{5}\\ = 3 - \sqrt 5 - \dfrac{{\sqrt 5 }}{5} = \dfrac{{15 - 5\sqrt 5 - \sqrt 5 }}{5} = \dfrac{{15 - 6\sqrt 5 }}{5}\end{array}\)
2.Giải các phương trình sau:
a) \(\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12\)
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
\(\begin{array}{l}\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12\\ \Leftrightarrow \sqrt {x - 1} + \sqrt {9\left( {x - 1} \right)} + \sqrt {4\left( {x - 1} \right)} = 12\\ \Leftrightarrow \sqrt {x - 1} + 3\sqrt {x - 1} + 2\sqrt {x - 1} = 12\\ \Leftrightarrow 6\sqrt {x - 1} = 12\\ \Leftrightarrow \sqrt {x - 1} = 2\\ \Leftrightarrow x - 1 = 4\\ \Leftrightarrow x = 5\left( {tmdk} \right)\end{array}\)
Vậy \(x = 5.\)
b) \(\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\)
ĐKXĐ: \(x - 5 \ge 0 \Leftrightarrow x \ge 5\)
\(\begin{array}{l}\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\\ \Leftrightarrow \sqrt {{x^2} - 5x} = \sqrt {x - 5} \\ \Leftrightarrow {x^2} - 5x = x - 5\\ \Leftrightarrow x\left( {x - 5} \right) - \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {ktm} \right)\\x = 5\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(x = 5\).
Bài II (VD):
Phương pháp:
a) Thay giá trị của \(x\) (tmđk) vào biểu thức và tính giá trị.
b) Quy đồng mẫu thức và rút gọn biểu thức.
c) Rút gọn \(P = A.B.\) Áp dụng BĐT Cô-si để tìm GTNN.
Cách giải:
Cho hai biểu thức \(A = \dfrac{{x + 7}}{{3\sqrt x }}\) và \(B = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x + 1}}{{\sqrt x - 3}} + \dfrac{{7\sqrt x + 3}}{{9 - x}}\) với \(x > 0;x \ne 9.\)
b) Tính \(A\) khi \(x = 25.\) .
Điều kiện: \(x > 0,\,\,x \ne 9.\)
Có:\(x = 25\) (tmđk)
Thay \(x = 25\) vào \(A\) ta được: \(A = \dfrac{{25 + 7}}{{3\sqrt {25} }} = \dfrac{{32}}{{15}}\)
Vậy khi \(x = 25\) thì \(A = \dfrac{{32}}{{15}}.\)
b) Rút gọn biểu thức \(B.\)
Điều kiện xác định: \(x > 0;x \ne 9.\)
\(\begin{array}{l}B = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x + 1}}{{\sqrt x - 3}} + \dfrac{{7\sqrt x + 3}}{{9 - x}}\\ = \dfrac{{2\sqrt x \left( {\sqrt x - 3} \right) + \left( {\sqrt x + 1} \right)\left( {\sqrt x + 3} \right) - \left( {7\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{2x - 6\sqrt x + x + 4\sqrt x + 3 - 7\sqrt x - 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3x - 9\sqrt x }}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x }}{{\sqrt x + 3}}\end{array}\)
Vậy \(B = \dfrac{{3\sqrt x }}{{\sqrt x + 3}}\) với \(x > 0;x \ne 9.\)
c) Tính giá trị nhỏ nhất của biểu thức \(P = AB.\)
Điều kiện xác định: \(x > 0;x \ne 9\)
\(P = A.B = \dfrac{{x + 7}}{{3\sqrt x }}.\dfrac{{3\sqrt x }}{{\sqrt x + 3}} = \dfrac{{x + 7}}{{\sqrt x + 3}}\)
\(\begin{array}{l} = \dfrac{{x - 9 + 16}}{{\sqrt x + 3}} = \dfrac{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}{{\sqrt x + 3}} + \dfrac{{16}}{{\sqrt x + 3}}\\ = \sqrt x - 3 + \dfrac{{16}}{{\sqrt x + 3}} = \left( {\sqrt x + 3} \right) + \dfrac{{16}}{{\sqrt x + 3}} - 6\end{array}\)
Áp dụng BĐT Cô –si cho hai số không âm \(\left( {\sqrt x + 3} \right)\) và \(\dfrac{{16}}{{\sqrt x + 3}}\) ta có:
\(\begin{array}{l}\left( {\sqrt x + 3} \right) + \dfrac{{16}}{{\sqrt x + 3}} \ge 2\sqrt {\left( {\sqrt x + 3} \right).\dfrac{{16}}{{\sqrt x + 3}}} \\ \Leftrightarrow \left( {\sqrt x + 3} \right) + \dfrac{{16}}{{\sqrt x + 3}} \ge 8\\ \Leftrightarrow \left( {\sqrt x + 3} \right) + \dfrac{{16}}{{\sqrt x + 3}} - 6 \ge 2\end{array}\)
Hay \(P \ge 2.\)
Dấu “=” xảy ra khi \(\sqrt x + 3 = \dfrac{{16}}{{\sqrt x + 3}} \Rightarrow {\left( {\sqrt x + 3} \right)^2} = 16\)
\( \Leftrightarrow \left[ \begin{array}{l}\sqrt x + 3 = 4\\\sqrt x + 3 = - 4\left( L \right)\end{array} \right. \Rightarrow \sqrt x = 1 \Leftrightarrow x = 1\left( {tm} \right)\)
Vậy giá trị nhỏ nhất của \(P\) là \(2 \Leftrightarrow x = 1.\)
Bài III (VD ):
Phương pháp:
a) Đồ thị hàm số \(y = ax + b\,\left( {a \ne 0} \right)\) là đường thẳng đi qua hai điểm có tọa độ \(\left( { - \dfrac{b}{a};0} \right)\) và \(\left( {0;b} \right)\)
b) Giải phương trình hoành độ giao điểm để tìm \(x\), từ đó thay trở lại hàm số để tìm tung độ giao điểm\(y.\)
c) Tìm điều kiện để ba đường thẳng cắt nhau.
Thay tọa độ giao điểm vừa tìm được ở câu \(b\) vào hàm số \(y = mx + 5\) ta tìm được \(m.\)
Cách giải:
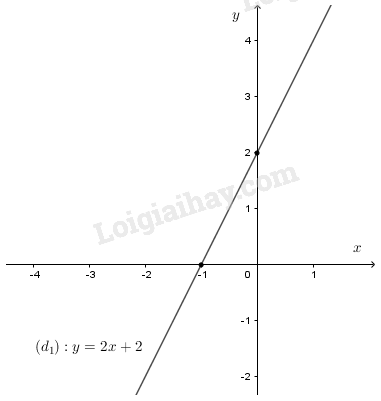
Cho đường thẳng \(\left( {{d_1}} \right):y = 2x + 2\)
a) Vẽ đường thẳng \(\left( {{d_1}} \right)\) trên mặt phẳng tọa độ \(Oxy.\)
Cho \(x = 0 \Rightarrow y = 2\)
\(y = 0 \Rightarrow x = - 1\)
Đồ thị hàm số \(y = 2x + 2\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0;2} \right)\)và \(\left( { - 1;0} \right)\)
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right):y = x - 3.\)
Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) ta có:
\(\begin{array}{l}2x + 2 = x - 3\\ \Leftrightarrow 2x - x = - 3 - 2\\ \Leftrightarrow x = - 5\end{array}\)
Thay \(x = - 5\) vào hàm số \(y = x - 3\) ta được \(y = - 5 - 3 = - 8\)
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\).
c) Cho đường thẳng \(\left( {{d_3}} \right):y = mx + 5.\) Tìm giá trị của \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\,\left( {{d_3}} \right)\) cắt nhau tại một điểm.
Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) cắt nhau thì \(m \ne \left\{ {1;2} \right\}\)
Theo câu b) ta có tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\).
Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) đồng quy thì điểm có tọa độ \(\left( { - 5; - 8} \right)\) cũng thuộc đường thẳng \(\left( {{d_3}} \right).\)
Thay \(x = - 5;y = - 8\) vào hàm số \(y = mx + 5\) ta được: \( - 8 = m\left( { - 5} \right) + 5 \Leftrightarrow m = \dfrac{{13}}{5}\) (thỏa mãn)
Vậy \(m = \dfrac{{13}}{5}.\)
Bài IV (VD ):
1.
Phương pháp:
Kẻ \(DH \bot b\) tại \(H.\) Sử dụng định nghĩa tỉ số lượng giác của góc nhọn để suy ra chiều rộng khúc sông.
Cách giải:
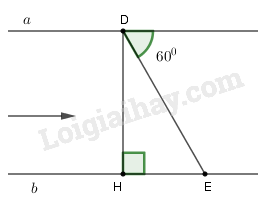
Kẻ \(DH \bot b\) tại \(H.\) Khi đó chiều rộng khúc sông là đoạn \(DH.\)
Đổi \(20\) phút \( = \dfrac{1}{3}h.\)
Độ dài đường đi của thuyền là \(DE = \dfrac{1}{3}.2 = \dfrac{2}{3}km\)
Ta có \(\widehat {HDE} = {90^0} - {60^0} = {30^0}\)
Xét tam giác \(DHE\) vuông tại \(H\), theo định nghĩa tỉ số lượng giác ta có:
\(\cos \widehat {HDE} = \dfrac{{DH}}{{DE}} \)\(\Rightarrow DH = DE.\cos {30^0} = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2} \)\(= \dfrac{{\sqrt 3 }}{3}\)
Vậy chiều rộng khúc sông là \(\dfrac{{\sqrt 3 }}{3}\,km.\)
2.
Phương pháp:
a) Chứng minh \(BC \bot OC\) dựa vào tính chất hai tam giác bằng nhau. Từ đó suy ra \(BC\) là tiếp tuyến của đường tròn thông qua định nghĩa tiếp tuyến.
b) Sử dụng tính chất hai tiếp tuyến cắt nhau, quan hệ từ vuông góc đến song song.
Tính chất hai tam giác đồng dạng.
c) Kẻ đường kính \(CP.\)
Sử dụng tính chất: Góc ngoài tại 1 đỉnh của tam giác bằng tổng hai góc trong không kề với đỉnh đó.
Sử dụng: Tổng bốn góc trong một tứ giác bằng \({360^0}.\)
Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác.
Cách giải:
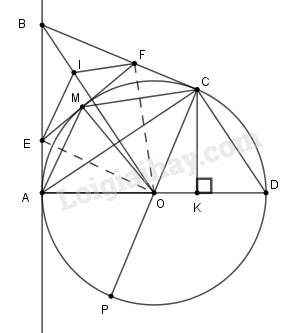
a) Chứng minh rằng : \(CB\) là tiếp tuyến của \(\left( O \right).\)
Xét \(\Delta ABO\) và \(\Delta CBO\) có:
+) \(AB = BC\left( {gt} \right)\)
+) \(BO\) cạnh chung
+) \(OA = OC\left( { = R} \right)\)
Nên \(\Delta ABO = \Delta CBO\left( {c - c - c} \right)\)
Suy ra \(\widehat {BCO} = \widehat {BAO} = {90^0}\), do đó: \(BC \bot OC\) tại \(C\).
Hay \(BC\) là tiếp tuyến của \(\left( {O;R} \right).\)
b) Vẽ đường kính \(AD\) của \(\left( O \right),\) kẻ \(CK\) vuông góc với \(AD.\)
Chứng minh rằng : \(CD//OB\) và \(BC.DC = CK.OB.\)
*) Xét đường tròn \(\left( {O;R} \right)\) có \(\Delta ACD\) nội tiếp đường tròn có cạnh \(AD\) là đường kính nên \(\Delta ACD\) vuông tại \(C.\)
Hay \(AC \bot CD\).
+) Xét đường tròn \(\left( {O;R} \right)\) có \(BA,BC\) là các tiếp tuyến cắt nhau tại \(B\) nên \(BA = BC\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra \(B\) thuộc đường trung trực của đoạn \(AC.\)
Lại có \(OA = OC = R\) nên \(O\) thuộc đường trung trực của đoạn \(AC.\)
Từ đó \(OB\) là đường trung trực của đoạn \(AC \Rightarrow OB \bot AC.\)
Lại có \(AC \bot CD\left( {cmt} \right)\) nên \(OB//CD.\)
*) Xét \(\Delta CKD\) và \(\Delta BAO\) có:
+) \(\widehat K = \widehat {BAO} = {90^0}\)
+) \(\widehat {CDK} = \widehat {AOB}\) (hai góc ở vị trí đồng vị)
Nên \(\Delta CDK\) đồng dạng với \(\Delta {\rm B}{\rm O}{\rm A}\left( {g - g} \right)\)
Suy ra \(\dfrac{{CK}}{{AB}} = \dfrac{{DC}}{{OB}} \Leftrightarrow OB.CK = DC.AB\)
Mà \(AB = BC\) (gt) nên \(OB.CK = BC.DC\)(đpcm)
c) Lấy \(M\) trên cung nhỏ \(AC\) của \(\left( O \right),\) vẽ tiếp tuyến tại \(M\) cắt \(AB,\,BC\) lần lượt tại \(E,\,\,F.\) Vẽ đường tròn tâm \(I\) nội tiếp tam giác \(BFE.\) Chứng minh rằng : \(\Delta MAC \backsim \Delta \,IFE.\)
Kẻ đường kính \(CP\) của \(\left( {O;R} \right)\)
Ta có: \(\widehat {POA}\) là góc ngoài của tam giác \(OAC\) nên \(\widehat {POA} = \widehat {OCA} + \widehat {OAC}\) mà \(\widehat {OAC} = \widehat {OCA}\) (do tam giác \(OCA\) cân tại \(O\)) nên \(\widehat {POA} = 2\widehat {ACO}.\)
Lại có \(\widehat {POM}\) là góc ngoài của tam giác \(OCM\) nên \(\widehat {POM} = \widehat {OCM} + \widehat {OMC}\) mà \(\widehat {OCM} = \widehat {OMC}\) (do tam giác \(OCM\) cân tại \(O\)) nên \(\widehat {POM} = 2\widehat {MCO}.\)
Do đó: \(\widehat {POM} - \widehat {POA} = 2\left( {\widehat {MCO} - \widehat {ACO}} \right)\) hay \(\widehat {MOA} = 2\widehat {MCA}.\)
Xét tứ giác \(EMOA\) có \(\widehat {EAO} = \widehat {EMO} = {90^0}\) (tính chất tiếp tuyến)
Nên \(\widehat {MOA} + \widehat {AEM} = {360^0} - \left( {\widehat {EAO} + \widehat {EMO}} \right) = {180^0}\)
Mà \(\widehat {AEM} + \widehat {BEF} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {MOA} = \widehat {BEF}\) (cùng bù với \(\widehat {AEM}\))
Lại có \(\widehat {BEF} = 2\widehat {IEF}\) (do \(I\) là tâm đường tròn nội tiếp tam giác \(BEF\))
Và \(\widehat {MOA} = 2\widehat {MCA}\) (cmt)
Suy ra \(\widehat {IEF} = \widehat {MCA}\)
Chứng minh tương tự:
Ta có \(\widehat {DOM}\) là góc ngoài của tam giác cân \(AOM \Rightarrow \widehat {DOM} = 2\widehat {MAO}\)
\(\widehat {DOC}\) là góc ngoài của tam giác cân \(AOC \Rightarrow \widehat {DOC} = 2\widehat {CAO}\)
Trừ vế với vế ta được: \(\widehat {MOC} = 2\widehat {MAC}\)
Lại có \(\widehat {MFC} + \widehat {MOC} = {360^0} - \left( {\widehat {FMO} - \widehat {CFO}} \right) = {180^0}\)
Và \(\widehat {MFC} + \widehat {BFE} = {180^0} \Rightarrow \widehat {BFE} = \widehat {COM}\)
Mà \(\widehat {COM} = 2\widehat {MAC};\widehat {BFE} = 2\widehat {IFE}\) nên \(\widehat {IFE} = \widehat {MAC}\)
Xét tam giác \(IEF\) và tam giác \(MCA\) có: \(\widehat {IFE} = \widehat {MAC}\) và \(\widehat {IEF} = \widehat {MCA}\) (cmt) nên \(\Delta IEF\) đồng dạng với \(\Delta MCA\)(đpcm).
Bài 5 (VDC ):
Phương pháp:
- Chia cả hai vế của đẳng thức đã cho cho \(xyz\).
- Đặt \(a = \dfrac{1}{x},b = \dfrac{1}{y},c = \dfrac{1}{z}\) đưa về tìm GTNN theo \(a,b,c\).
- Sử dụng bất đẳng thức \({a^2} + {b^2} \ge 2ab\).
Cách giải:
Ta có: \(xy + yz + zx = 3xyz\)
Chia cả hai vế cho \(xyz \ne 0\) ta được: \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 3\).
Đặt \(a = \dfrac{1}{x},b = \dfrac{1}{y},c = \dfrac{1}{z}\left( {a,b,c > 0} \right)\) thì \(a + b + c = 3\).
Khi đó \(\dfrac{{{x^2}}}{{z\left( {{z^2} + {x^2}} \right)}} = \dfrac{{{{\left( {\dfrac{1}{a}} \right)}^2}}}{{\dfrac{1}{c}.\left( {\dfrac{1}{{{c^2}}} + \dfrac{1}{{{a^2}}}} \right)}} = \dfrac{{{c^3}}}{{{a^2} + {c^2}}}\) \( = \dfrac{{{c^3} + c{a^2} - c{a^2}}}{{{c^2} + {a^2}}} = c - \dfrac{{c{a^2}}}{{{c^2} + {a^2}}}\)
\(\dfrac{{{y^2}}}{{x\left( {{x^2} + {y^2}} \right)}} = \dfrac{{{{\left( {\dfrac{1}{b}} \right)}^2}}}{{\dfrac{1}{a}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}} = \dfrac{{{a^3}}}{{{a^2} + {b^2}}}\) \( = \dfrac{{{a^3} + a{b^2} - a{b^2}}}{{{a^2} + {b^2}}} = a - \dfrac{{a{b^2}}}{{{a^2} + {b^2}}}\)
\(\dfrac{{{z^2}}}{{y\left( {{y^2} + {z^2}} \right)}} = \dfrac{{{{\left( {\dfrac{1}{c}} \right)}^2}}}{{\dfrac{1}{b}\left( {\dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)}} = \dfrac{{{b^3}}}{{{b^2} + {c^2}}}\)\( = \dfrac{{{b^3} + b{c^2} - b{c^2}}}{{{b^2} + {c^2}}} = b - \dfrac{{b{c^2}}}{{{b^2} + {c^2}}}\)
\( \Rightarrow A = c - \dfrac{{c{a^2}}}{{{c^2} + {a^2}}} + a - \dfrac{{a{b^2}}}{{{a^2} + {b^2}}} + b - \dfrac{{b{c^2}}}{{{b^2} + {c^2}}}\)
\( = \left( {a + b + c} \right) - \left( {\dfrac{{c{a^2}}}{{{c^2} + {a^2}}} + \dfrac{{a{b^2}}}{{{a^2} + {b^2}}} + \dfrac{{b{c^2}}}{{{b^2} + {c^2}}}} \right)\)
\( = 3 - \left( {\dfrac{{c{a^2}}}{{{c^2} + {a^2}}} + \dfrac{{a{b^2}}}{{{a^2} + {b^2}}} + \dfrac{{b{c^2}}}{{{b^2} + {c^2}}}} \right)\)
Mà \({c^2} + {a^2} \ge 2ca \Rightarrow \dfrac{{c{a^2}}}{{{c^2} + {a^2}}} \le \dfrac{{c{a^2}}}{{2ca}} = \dfrac{a}{2}\)
Tương tự \(\dfrac{{a{b^2}}}{{{a^2} + {b^2}}} \le \dfrac{b}{2}\) và \(\dfrac{{b{c^2}}}{{{b^2} + {c^2}}} \le \dfrac{c}{2}\)
\( \Rightarrow \dfrac{{c{a^2}}}{{{c^2} + {a^2}}} + \dfrac{{a{b^2}}}{{{a^2} + {b^2}}} + \dfrac{{b{c^2}}}{{{b^2} + {c^2}}} \le \dfrac{a}{2} + \dfrac{b}{2} + \dfrac{c}{2} = \dfrac{3}{2}\)
\( \Rightarrow 3 - \left( {\dfrac{{c{a^2}}}{{{c^2} + {a^2}}} + \dfrac{{a{b^2}}}{{{a^2} + {b^2}}} + \dfrac{{b{c^2}}}{{{b^2} + {c^2}}}} \right) \ge 3 - \dfrac{3}{2} = \dfrac{3}{2}\).
Vậy \(A \ge \dfrac{3}{2}\) nên \(\min A = \dfrac{3}{2}\).
Dấu “=” xảy ra khi \(a = b = c = 1\).
Hết