Giải đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Tây Hồ — Không quảng cáo

Đề bài

Câu 1 (2,0 điểm):

Cho các biểu thức $A = \dfrac{{\sqrt x }}{{\sqrt x  + 1}}$ và $B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{5}{{\sqrt x  + 1}} + \dfrac{{2\sqrt x  - 4}}{{x - 1}}$ với $x > 0,\,\,x \ne 1$

a) Tính giá trị của biểu thức $A$  khi $x = 9.$

b) Chứng minh $B = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}.$

c) Tìm giá trị của $x$ để $\dfrac{B}{A} < \dfrac{3}{4}.$

Câu 2 (2,5 điểm):

1. Giải bài toán bằng cách phương trình hoặc hệ phương trình:

Một xe ô tô con và một xe ô tô tải khởi hành cùng một lúc đi từ A đến B. Vận tốc của xe ô tô con lớn hơn vận tốc của xe ô tô tải là 10  km/h nên xe ô tô con đến B sớm hơn xe ô tô tải là 30 phút. Tính vận tốc của mỗi xe biết quãng đường AB dài 100 km.

2. Bài toán thực tế:

Một cửa hàng phục vụ hai loại bánh pizza có dạng hình trụ, độ dày giống nhau nhưng khác nhau về kích thước. Loại nhỏ có đường kính 30 cm giá 60000 đồng, loại lớn có đường kính 40 cm giá 80000 đồng. Vậy mua cái nào lợi hơn? Vì sao?

Câu 3 (1,5 điểm):

1. Giải hệ phương trình: $\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} =  - 2\end{array} \right.$

2. Cho parabol $\left( P \right):\,\,\,y = {x^2}$ và đường thẳng $\left( d \right):\,\,\,\,y = mx + 2$

a) Với $m =  - 1$. Tìm tọa độ các giao điểm của $\left( P \right)$ và $\left( d \right).$

b) Tìm các giá trị của $m$ để $\left( d \right)$  cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},\,\,{x_2}$ sao cho ${x_1} - 2{x_2} = 5.$

Câu 4 (3,0 điểm):

Cho $\Delta ABC$ có ba góc nhọn. Vẽ đường tròn $\left( O \right)$  đường kính $BC,$ đường tròn cắt $AB$ và $AC$  lần lượt ở $D$  và $E;\,\,BE$ và $CD$ cắt nhau tại $H.$

a) Chứng minh tứ giác $ADHE$  nội tiếp

b) Chứng minh $AC.AE = AB.AD.$

c) $AH$ kéo dài cắt $BC$ tại $F.$ Chứng minh rằng $H$ là tâm đường tròn nội tiếp $\Delta DEF.$

Câu 5 (0,5 điểm): Cho hai số dương $x,\,y$, có $x + y = 1$.

Tìm giá trị nhỏ nhất của biểu thức $B = \left( {1 - \dfrac{1}{{{x^2}}}} \right)\left( {1 - \dfrac{1}{{{y^2}}}} \right).$

LG câu 1

Phương pháp giải:

a) Thay $x = 9$ vào $A$ và tính.

b) Quy đồng mẫu thức, thực hiện phép cộng trừ phân thức và rút gọn.

c) Giải bất phương trình $\dfrac{B}{A} < \dfrac{3}{4}$. Chú ý đối chiếu điều kiện.

Lời giải chi tiết:

Cho các biểu thức $A = \dfrac{{\sqrt x }}{{\sqrt x  + 1}}$ và $B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{5}{{\sqrt x  + 1}} + \dfrac{{2\sqrt x  - 4}}{{x - 1}}$ với $x > 0,\,\,x \ne 1$

a) Tính giá trị của biểu thức A khi $x = 9$

Thay $x = 9\,\,\,\left( {tm} \right)$ vào $A$ được $A = \dfrac{{\sqrt 9 }}{{\sqrt 9  + 1}} = \dfrac{3}{4}$

Vậy với $x = 9$ thì $A = \dfrac{3}{4}.$

b) Chứng minh $B = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}$

Điều kiện: $x > 0,\,\,\,x \ne 1.$

$B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{5}{{\sqrt x  + 1}} + \dfrac{{2\sqrt x  - 4}}{{x - 1}}$$\, + \dfrac{{2\sqrt x  - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}$

$= \dfrac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} - \dfrac{{5\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}$

$\begin{array}{l} = \dfrac{{{{\left( {\sqrt x } \right)}^2} + \sqrt x  - 5\sqrt x  + 5 + 2\sqrt x  - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\\,\,\,\,\, = \dfrac{{{{\left( {\sqrt x } \right)}^2} - 2\sqrt x  + 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\\,\,\,\,\, = \dfrac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\,\\ = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\end{array}$

Vậy $B = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}$  với mọi $x > 0,\,\,x \ne 1.$

c) Tìm giá trị của $x$ để $\dfrac{B}{A} < \dfrac{3}{4}.$

Điều kiện: $x > 0,\,\,x \ne 1$

$\begin{array}{l}\dfrac{B}{A} < \dfrac{3}{4}\\ \Leftrightarrow \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}:\dfrac{{\sqrt x }}{{\sqrt x  + 1}} < \dfrac{3}{4}\\ \Leftrightarrow \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}.\dfrac{{\sqrt x  + 1}}{{\sqrt x }} < \dfrac{3}{4}\\ \Leftrightarrow \dfrac{{\sqrt x  - 1}}{{\sqrt x }} - \dfrac{3}{4} < 0\\ \Leftrightarrow \dfrac{{4\sqrt x  - 4 - 3\sqrt x }}{{4\sqrt x }} < 0\\ \Leftrightarrow \dfrac{{\sqrt x  - 4}}{{4\sqrt x }} < 0\,\,\,\,\,\,\,\left( * \right)\end{array}$

Do $x > 0 \Rightarrow 4\sqrt x  > 0 \Rightarrow \left( * \right)$$\Leftrightarrow \sqrt x  - 4 < 0 \Leftrightarrow \sqrt x  < 4$ $\Leftrightarrow x < 16$

Với $x > 0,x \ne 1$$\Rightarrow \left\{ \begin{array}{l}0 < x < 16\\x \ne 1\end{array} \right.$

Vậy để $\dfrac{B}{A} < \dfrac{3}{4}$ thì $\left\{ \begin{array}{l}0 < x < 16\\x \ne 1\end{array} \right..$

LG câu 2

Phương pháp giải:

1. Giải bài toán bằng cách lập phương trình:

Gọi vận tốc của xe ô tô con là $x\,\,\,\left( {km/h} \right),\,\,\,\,\left( {x > 10} \right).$

Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.

Từ đó lập phương trình, giải phương trình.

Đối chiếu với điều kiện rồi kết luận.

2. Bài toán thực tế

Bước 1: Tính bán kính của mỗi loại bánh và diện tích tương ứng.

Bước 2: Tính giá tiền trên $1\,\,c{m^2}$ của mỗi loại bánh.

Bước 3: So sánh giá tiền trên $1\,c{m^2}$ của mỗi loại bánh (giá bánh nào cao hơn là đắt hơn).

Lời giải chi tiết:

1. Giải bài toán bằng cách phương trình hoặc hệ phương trình

Gọi vận tốc của xe ô tô con là $x\,\,\,\left( {km/h} \right),\,\,\,\,\left( {x > 10} \right).$

Vận tốc của xe ô tô con lớn hơn vận tốc của xe tải là $10\,km/h$ nên vận tốc xe tải là: $x - 10\,\,\,\left( {km/h} \right).$

Thời gian xe ô tô con đi hết quãng đường AB là: $\dfrac{{100}}{x}\,\,\left( h \right).$

Thời gian xe tải đi hết quãng đường AB là: $\dfrac{{100}}{{x - 10}}\,\,\,\left( h \right)$

Xe ô tô đến B sớm hơn xe tải $30$ phút $= \dfrac{1}{2}\,\,\left( h \right)$ nên ta có phương trình:

$\begin{array}{l}\,\,\,\,\,\,\,\,\,\dfrac{{100}}{{x - 10}} - \dfrac{{100}}{x} = \dfrac{1}{2}\\ \Leftrightarrow 2.100x - 2.100\left( {x - 10} \right) = x\left( {x - 10} \right)\\ \Leftrightarrow 200x - 200x + 2000 = {x^2} - 10x\\ \Leftrightarrow {x^2} - 10x - 2000 = 0\\ \Leftrightarrow {x^2} - 50x + 40x - 2000 = 0\\ \Leftrightarrow x\left( {x - 50} \right) + 40\left( {x - 50} \right) = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {x + 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 50 = 0\\x + 40 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 50\,\,\,\left( {tm} \right)\\x =  - 40\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}$

Vậy vận tốc của xe ô tô con là $50\,\,km/h$ và vận tốc của ô tô tải là: $50 - 10 = 40\,\,km/h.$

2. Bài toán thực tế

Bánh pizza loại nhỏ có đường kính 30cm thì có bán kính là 15cm

$\Rightarrow$ Bánh loại nhỏ có diện tích là: ${15^2}\pi \,\left( {c{m^2}} \right)$.

Giá tiền trên $1\,c{m^2}$ của bánh loại nhỏ là $\dfrac{{60000}}{{{{15}^2}\pi }} = \dfrac{{4000}}{{15\pi }}$ (đồng)

Bánh pizza loại to có đường kính 40cm thì có bán kính là 20cm

$\Rightarrow$ Bánh loại to có diện tích ${20^2}\pi \,\left( {c{m^2}} \right)$.

Giá tiền trên $1\,c{m^2}$ của bánh loại to là $\dfrac{{80000}}{{{{20}^2}\pi }} = \dfrac{{4000}}{{20\pi }}$ (đồng)

Ta có $\dfrac{{4000}}{{15\pi }} > \dfrac{{4000}}{{20\pi }}$ nên giá tiền trên $1\,c{m^2}$ của bánh loại nhỏ đắt hơn bánh loại to.

Vậy mua bánh loại to lợi hơn.

LG câu 3

Phương pháp giải:

1. Tìm điều kiện xác định của hệ phương trình.

Đặt $\left\{ \begin{array}{l}u = \dfrac{1}{{x - 2}}\\v = \dfrac{1}{{3y + 1}}\end{array} \right.$. Giải hệ phương trình được $u,v \Rightarrow x,y$ đối chiếu điều kiện và kết luận.

2a) Thay $m =  - 1$ vào phương trình đường thẳng $d.$

Xét phương trình hoành độ giao điểm của hai đồ thị và giải phương trình tìm $x \Rightarrow y$ ta được tọa độ các giao điểm của $\left( P \right)$  và $\left( d \right).$

2b) Xét phương trình hoành độ giao điểm $\left( * \right)$ của hai đồ thị hàm số.

Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt $\Leftrightarrow \left( * \right)$ có hai nghiệm phân biệt $\Leftrightarrow \Delta  > 0.$

Sử dụng điều kiện ${x_1} - 2{x_2} = 5$ và áp dụng hệ thức Viét $\left\{ \begin{array}{l}S = {x_1} + {x_2} = \dfrac{{ - b}}{a}\\P = {x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.$  (với ${x_1};{x_2}$ là 2 nghiệm của phương trình $\left( * \right)$)để giải tìm $m.$

Đối chiếu với điều kiện có nghiệm rồi kết luận.

Lời giải chi tiết:

1. Giải hệ phương trình: $\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} + \dfrac{4}{{3y + 1}} = 5\\\dfrac{2}{{x - 2}} - \dfrac{4}{{3y + 1}} =  - 2\end{array} \right.$

Điều kiện: $x \ne 2,\,\,\,y \ne  - \dfrac{1}{3}.$

Đặt  $\left\{ \begin{array}{l}u = \dfrac{1}{{x - 2}}\\v = \dfrac{1}{{3y + 1}}\end{array} \right..$  Khi đó ta có hệ phương trình

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}u + 4v = 5\\2u - 4v =  - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3u = 3\\u + 4v = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 1\\v = 1\end{array} \right.\end{array}$

$\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{{x - 2}} = 1\\\dfrac{1}{{3y + 1}} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 1\\3y + 1 = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3\,\,\,\,\left( {tm} \right)\\y = 0\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy nghiệm của hệ phương trình là $\left( {x;y} \right) = \left( {3;0} \right).$

2. Cho parabol $\left( P \right):\,\,\,y = {x^2}$ và đường thẳng $\left( d \right):\,\,\,\,y = mx + 2$

a) Với $m =  - 1$ . Tìm tọa độ các giao điểm của $\left( P \right)$ và $\left( d \right).$

Thay $m =  - 1$ vào phương trình đường thẳng $\left( d \right)$ ta được: $y =  - x + 2$

Xét phương trình hoành độ giao điểm của $\left( P \right)$ và $\left( d \right)$ ta có:

$\begin{array}{l}{x^2} =  - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right.\end{array}$

Vậy với $m =  - 1$ thì $\left( d \right)$ cắt $\left( P \right)$ tại 2 điểm phân biệt $\left( { - 2;4} \right);\,\,\,\left( {1;1} \right).$

b) Tìm các giá trị của $m$ để $\left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},\,\,{x_2}$ sao cho ${x_1} - 2{x_2} = 5.$

Xét phương trình hoành độ giao điểm của $\left( P \right)$  và $\left( d \right)$ ta có:

${x^2} = mx + 2$$\Leftrightarrow {x^2} - mx - 2 = 0\,\,\,\left( * \right)$

Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt $\Leftrightarrow \left( * \right)$ có hai nghiệm phân biệt $\Leftrightarrow \Delta  > 0$

$\Leftrightarrow {m^2} + 8 > 0$

Ta có: ${m^2} + 8 > 0\,$với mọi $m$

$\Rightarrow \left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},\,\,{x_2}$ với mọi $m.$

Khi đó ta có: ${x_1},\,\,{x_2}$ là hai nghiệm của phương trình $\left( * \right).$

Áp dụng hệ thức Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = m\,\,\,\,\left( 1 \right)\\{x_1}{x_2} =  - 2\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.$

Theo giả thiết ta có:  ${x_1} - 2{x_2} = 5\,\,\,\left( 3 \right)$

Từ $\left( 1 \right)$ và $\left( 3 \right)$ ta có hệ phương trình:$\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1} - 2{x_2} = 5\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}{x_1} = m - {x_2}\\3{x_2} = m - 5\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}{x_1} = \dfrac{{2m + 5}}{3}\\{x_2} = \dfrac{{m - 5}}{3}\end{array} \right.$

Thay ${x_1},\,\,{x_2}$ vào $\left( 2 \right)$ ta được:

$\begin{array}{l}\dfrac{{2m + 5}}{3}.\dfrac{{m - 5}}{3} =  - 2\\ \Leftrightarrow \left( {2m + 5} \right)\left( {m - 5} \right) =  - 18\\ \Leftrightarrow 2{m^2} - 10m + 5m - 25 + 18 = 0\\ \Leftrightarrow 2{m^2} - 5m - 7 = 0\\ \Leftrightarrow 2{m^2} - 7m + 2m - 7 = 0\end{array}$

$\begin{array}{l} \Leftrightarrow m\left( {2m - 7} \right) + \left( {2m - 7} \right) = 0\\ \Leftrightarrow \left( {2m - 7} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m - 7 = 0\\m + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{7}{2}\\m =  - 1\end{array} \right.\end{array}$

Vậy với $\left[ \begin{array}{l}m =  - 1\\m = \dfrac{7}{2}\end{array} \right.$ thỏa mãn yêu cầu đề bài

LG câu 4

Phương pháp giải:

a) Chứng minh tứ giác $ADHE$ có tổng hai góc đối $\angle ADH;\angle AEH$ bằng $180^\circ$

b) Chứng minh $\Delta ABE \backsim \Delta ACD\,\,\left( {g - g} \right)$ suy ra tỉ lệ $\Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AC}}{{AD}}$$\Leftrightarrow AB.AD = AC.AE$

c) Chứng minh tứ giác $HECF$ nội tiếp suy ra $\Rightarrow \angle HEF = \angle HCF$ mà $BDEC$ là tứ giác nội tiếp có $\angle HCF = \angle DEB.$

$\Rightarrow \angle HEF = \angle DEB \Rightarrow EH$ là phân giác $\angle DEF$

Chứng minh tương tự $DH$ là phân giác $\angle EDF$

Suy ra $H$  là giao 2 đường phân giác của $\Delta DEF \Rightarrow H$ là tâm đường tròn nội tiếp $\Delta DEF.$

Lời giải chi tiết:

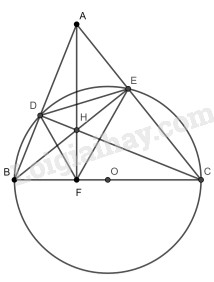
a) Chứng minh tứ giác $ADHE$ nội tiếp.

Ta có: $\angle BDC,\,\,\angle BEC$ là các góc nội tiếp chắn nửa đường tròn $\left( O \right)$

$\Rightarrow \angle BDC = \angle BEC = {90^0}$

Xét tứ giác $ADHE$ ta có: $\angle ADE + \angle AEH$ $= {90^0} + {90^0} = {180^0}$

Mà hai góc này là hai góc đối nhau

$\Rightarrow ADHE$ là tứ giác nội tiếp (dhnb).

b) Chứng minh $AC.AE = AB.AD.$

Xét $\Delta ABE$ và $\Delta ACD$ có:

$\begin{array}{l}\angle AEB = \angle ADC\left( { = {{90}^0}} \right)\\\angle BAC\,\,chung\\ \Rightarrow \Delta ABE \backsim \Delta ACD\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AC}}{{AD}}\end{array}$

$\Leftrightarrow AB.AD = AC.AE\,$ (đpcm)

c) $AH$ kéo dài cắt $BC$ tại $F.$ Chứng minh rằng $H$ là tâm đường tròn nội tiếp $\Delta DEF.$

Do $\angle BDC = \angle BEC = 90^\circ \left( {cmt} \right)$$\Rightarrow \left\{ \begin{array}{l}CD \bot AB\\BE \bot AC\end{array} \right.$

Mà $BE \cap CD = H$ $\Rightarrow H$ là trực tâm $\Delta ABC.$

Lại có: $F \in AH$$\Rightarrow AF \bot BC$$\Rightarrow \angle HFC = 90^\circ$

$\Rightarrow \angle HFC + \angle BEC$$= 90^\circ  + 90^\circ  = 180^\circ$

$\Rightarrow HECF$ là tứ giác nội tiếp (dhnb)

$\Rightarrow \angle HEF = \angle HCF$ (hai góc nội tiếp cùng chắn cung $HF$)

Mà $BDEC$ là tứ giác nội tiếp có $\angle HCF = \angle DEB$ (hai góc nội tiếp cùng chắn cung $BD$)

$\Rightarrow \angle HEF = \angle DEB$$\Rightarrow EH$ là phân giác $\angle DEF$

Chứng minh tương tự ta có: $DH$ là phân giác

$\Rightarrow H$ là giao 2 đường phân giác của $\Delta DEF$

$\Rightarrow H$ là tâm đường tròn nội tiếp $\Delta DEF.$

LG câu 5

Phương pháp giải:

Rút gọn biểu thức $B.$

Áp dụng bất đẳng thức Cô-si cho hai số dương $x,y$ ta được:

$x + y \ge 2\sqrt {xy}$$\Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy$$\Leftrightarrow \dfrac{1}{4} \le xy$$\Rightarrow 9 \le 1 + \dfrac{2}{{xy}}$

Vậy B đạt giá trị nhỏ nhất bằng 9

Lời giải chi tiết:

Cho hai số dương $x,\,y$ , có $x + y = 1$ . Tìm giá trị nhỏ nhất của biểu thức $B = \left( {1 - \dfrac{1}{{{x^2}}}} \right)\left( {1 - \dfrac{1}{{{y^2}}}} \right).$

$\begin{array}{l}B = \left( {1 - \dfrac{1}{{{x^2}}}} \right)\left( {1 - \dfrac{1}{{{y^2}}}} \right)\\ = \dfrac{{{x^2} - 1}}{{{x^2}}}.\dfrac{{{y^2} - 1}}{{{y^2}}}\\\,\,\,\, = \dfrac{{{x^2}{y^2} - \left( {{x^2} + {y^2}} \right) + 1}}{{{x^2}.{y^2}}}\\\,\,\,\, = \dfrac{{{x^2}{y^2} - {{\left( {x + y} \right)}^2} + 2xy + 1}}{{{x^2}{y^2}}}\\\,\,\,\, = \dfrac{{{x^2}{y^2} - 1 + 2xy + 1}}{{{x^2}{y^2}}} = 1 + \dfrac{2}{{xy}}\end{array}$

Áp dụng BĐT Cô-si cho 2 số dương $x,\,y$ ta có: $x + y \ge 2\sqrt {xy}$$\Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy$

$\begin{array}{l} \Leftrightarrow 1 \ge 4xy \Leftrightarrow \dfrac{1}{4} \ge xy \Leftrightarrow \dfrac{2}{{\dfrac{1}{4}}} \le \dfrac{2}{{xy}}\\ \Leftrightarrow 8 \le \dfrac{2}{{xy}} \Leftrightarrow 9 \le 1 + \dfrac{2}{{xy}}\end{array}$

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y = 1\end{array} \right.$ $\Leftrightarrow x = y = \dfrac{1}{2}$

Vậy B đạt giá trị nhỏ nhất bằng 9 khi $x = y = \dfrac{1}{2}.$