Giải đề thi học kì 1 toán lớp 9 năm 2020 - 2021 quận Tây Hồ — Không quảng cáo

Bài 1 (2 điểm)

Cho $A = \frac{{20 - 2\sqrt x }}{{x - 25}} + \frac{3}{{\sqrt x  + 5}}$ và $B = \frac{{\sqrt x  + 2}}{{\sqrt x  - 5}}$(với $x \ge 0\,;\,\,x \ne 5$).

a) Tính giá trị của biểu thức B khi x=49.

b) Rút gọn A

c) Tìm giá trị của x để $B:A = \left| {x - 4} \right|.$

Bài 2 (2 điểm)

Cho hàm số bậc nhất $y = \left( {2m - 1} \right)x - 2m + 5$($m$ là tham số) có đồ thị là đường thẳng $\left( d \right)$ và hàm số $y = 2x + 1$ có đồ thị là đường thẳng $\left( {d'} \right)$.

a) Tìm giá trị của $m$ để đường thẳng $\left( d \right)$ đi qua điểm $A\left( {2;\, - 3} \right).$

b) Tìm giá trị của $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $\left( {d'} \right)$. Với giá trị của $m$ vừa tìm được, vẽ đường thẳng $\left( d \right)$ và tính góc $\alpha$ tạo bởi đường thẳng $\left( d \right)$ và trục $Ox$ (làm tròn đến phút).

Bài 3 (2 điểm)

Giải phương trình:

a) $\sqrt {4x - 8}  - \sqrt {25x - 50}  = 3 - \sqrt {16x - 32}$

b) $\sqrt {2x - 1}  + \sqrt {4{x^2} - 1}  = 0.$

Bài 4 (3 điểm)

Cho đường tròn $\left( {O;\,R} \right)$, đường kính AB. Qua điểm $A$ và điểm $B$ lần lượt vẽ đường thẳng $d$ và $d'$ là hai tiếp tuyến của đường tròn. Lấy điểm $M$ bất kì thuộc đường tròn $\left( O \right)$ ($M$ khác $A$ và $B$). Qua $M$ kẻ tiếp tuyến với đường tròn $\left( O \right)$ cắt $d$ và $d'$ theo thứ tự tại C và D.

a) Chứng minh bốn điểm $A,\,C,\,M,\,O$ thuộc một đường tròn.

b) Chứng minh $\Delta OCD$ vuông và $4.AC.BD = A{B^2}$.

c) Chứng minh $AB$ là tiếp tuyến của đường tròn ngoại tiếp $\Delta OCD$.

Bài 5 (1 điểm)

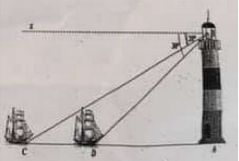
a) Một người đứng trên ngọn hải đăng cao 100 mét quan sát hai lần một con thuyền đang đi về phía ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là ${20^0}$, lần thứ hai người đó nhìn thấy thuyền với góc hạ là ${30^0}$. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến mét).

b) Cho các số thực dương $x,\,y$ thỏa mãn $xy > 2020x + 2021y$.

Chứng minh rằng: $x+y > (\sqrt {2020}+\sqrt {2021})^2$

LỜI GIẢI CHI TIẾT

Bài 1:

a) Thay $x = 49$(t/m điều kiện) vào $B$ ta được:

$B = \frac{{\sqrt {49}  + 2}}{{\sqrt {49}  - 5}} = \frac{9}{2}$

Vậy $B = \frac{9}{2}$ khi $x = 49$.

b)

$\begin{array}{l}A = \frac{{20 - 2\sqrt x }}{{x - 25}} + \frac{3}{{\sqrt x  + 5}}\\A = \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}} + \frac{{3\left( {\sqrt x  - 5} \right)}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\\A = \frac{{20 - 2\sqrt x  + 3\sqrt x  - 15}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\\A = \frac{{\sqrt x  + 5}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\\A = \frac{1}{{\sqrt x  - 5}}\end{array}$

Vậy $A = \frac{1}{{\sqrt x  - 5}}$.

c) Ta có:

$\begin{array}{l}B:A = \left| {x - 4} \right|\\ \Leftrightarrow \frac{{\sqrt x  + 2}}{{\sqrt x  - 5}}:\frac{1}{{\sqrt x  - 5}} = \left| {x - 4} \right|\\ \Leftrightarrow \frac{{\sqrt x  + 2}}{{\sqrt x  - 5}}.\left( {\sqrt x  - 5} \right) = \left| {x - 4} \right|\\ \Leftrightarrow \sqrt x  + 2 = \left| {x - 4} \right|\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt x  + 2 = x - 4}\\{ - \sqrt x  - 2 = x - 4}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \sqrt x  - 6 = 0}\\{x + \sqrt x  - 2 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 2} \right) = 0}\\{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right) = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt x  - 3 = 0}\\{\sqrt x  - 1 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 9\,(t/m)}\\{x = 1\,(t/m)}\end{array}} \right.\end{array}$

Vậy $x \in \left\{ {1;\,9} \right\}$ thỏa mãn đề bài

Bài 2:

a) $\left( d \right)$ đi qua điểm $A\left( {2;\, - 3} \right)$ khi:

$\begin{array}{l}\left( {2m - 1} \right).2 - 2m + 5 =  - 3\\ \Leftrightarrow 2m =  - 6\\ \Leftrightarrow m =  - 3\end{array}$

Vậy $m =  - 3$.

b) $\left( d \right)$//$\left( {d'} \right)$ khi và chỉ khi:

$\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{2m - 1 = 2}\\{ - 2m + 5 \ne 1}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = \frac{3}{2}}\\{m \ne 2}\end{array}} \right.\\ \Leftrightarrow m = \frac{3}{2}\end{array}$

Thay $m = \frac{3}{2}$ vào $\left( d \right)$ ta có: $y = 2x + 2$

+) Với x=-1 thì y=0 => $\left( d \right)$ đi qua điểm $\left( { - 1;\,0} \right)$

+) Với x=0 thì y=2 => $\left( d \right)$ đi qua điểm $\left( {0;\,2} \right)$

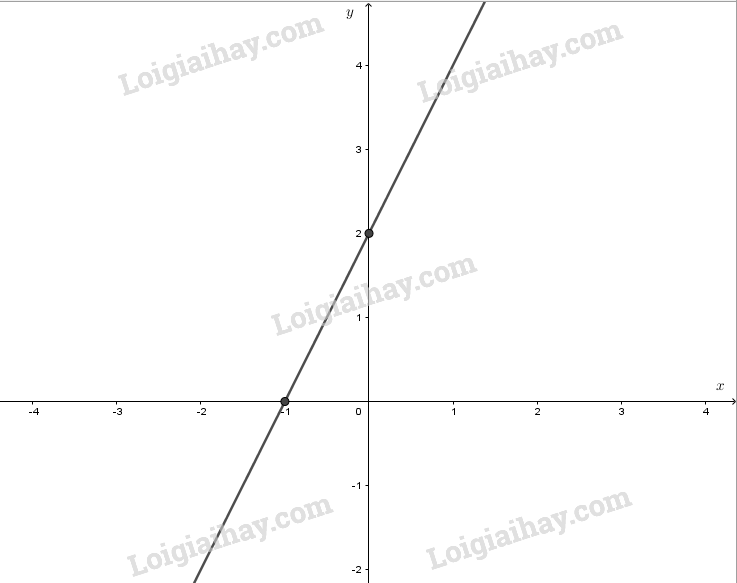
Ta có:

$\begin{array}{l}\tan \alpha  = \frac{2}{1} = 2\\ \Rightarrow \alpha  \approx {63^0}26'\end{array}$

Vậy $\alpha  \approx {63^0}26'$

Bài 3:

a) $\sqrt {4x - 8}  - \sqrt {25x - 50}  = 3 - \sqrt {16x - 32}$ đk: $x \ge 2$

$\begin{array}{l} \Leftrightarrow \sqrt {4\left( {x - 2} \right)}  - \sqrt {25\left( {x - 2} \right)}  = 3 - \sqrt {16\left( {x - 2} \right)} \\ \Leftrightarrow 2\sqrt {x - 2}  - 5\sqrt {x - 2}  = 3 - 4\sqrt {x - 2} \\ \Leftrightarrow \sqrt {x - 2}  = 3\\ \Leftrightarrow x - 2 = 9\\ \Leftrightarrow x = 11\,\left( {t/m} \right)\end{array}$

Vậy $x = 11$

b) $\sqrt {2x - 1}  + \sqrt {4{x^2} - 1}  = 0$ đk: $x \ge \frac{1}{2}$

$\begin{array}{l} \Leftrightarrow \sqrt {2x - 1}  + \sqrt {\left( {2x - 1} \right)\left( {2x + 1} \right)}  = 0\\ \Leftrightarrow \sqrt {2x - 1} .\left( {1 + \sqrt {2x + 1} } \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt {2x - 1}  = 0}\\{1 + \sqrt {2x + 1}  = 0\,\left( {VN} \right)}\end{array}} \right.\\ \Leftrightarrow 2x - 1 = 0\\ \Leftrightarrow x = \frac{1}{2}\,\left( {t/m} \right)\end{array}$

Bài 4:

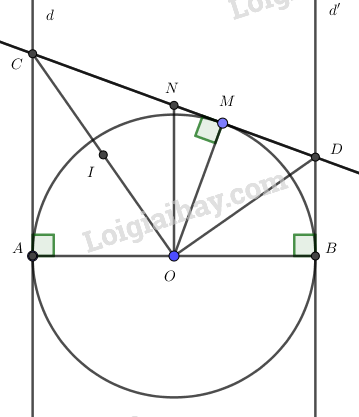
a) Gọi $I$ là trung điểm của $CO$

Do $d$ là tiếp tuyến của $\left( O \right)$ tại $A$ nên $\widehat {OAC} = {90^0}$

$d'$ là tiếp tuyến của $\left( O \right)$ tại M nên $\widehat {OMC} = {90^0}$

Xét tam giác $MCO$ vuông tại M có $MI$ là trung tuyến nên: $IC = IO = IM\,\left( 1 \right)$

Xét tam giác ACO vuông tại A có $AI$ là trung tuyến nên: $IA = IC = IO\,\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra: $IA = IC = IM = IO$

Vậy bốn điểm $A,C,\,M,\,O$ cùng thuộc một đường tròn

b) Ta có $OC$ là phân giác của $\widehat {AMO}$ nên: $\widehat {AOC} = \widehat {MCO}$

$OD$ là phân giác của $\widehat {BMO}$ nên: $\widehat {BOD} = \widehat {MOD}$

$\Rightarrow \,\,\widehat {MOC} + \widehat {DOM} = \widehat {AOC} + \widehat {BOD}$

Mà: $\,\widehat {MOC} + \widehat {DOM} + \widehat {AOC} + \widehat {BOD} = {180^0}$

Nên: $\,\,\widehat {MOC} + \widehat {DOM} = \widehat {AOC} + \widehat {BOD} = \frac{{{{180}^0}}}{2} = {90^0}$

$\Rightarrow \,\,\widehat {COD} = {90^0}$

Vậy tam giác $COD$ vuông tại O.

Do $AC$ và $MC$ là hai tiếp tuyến cắt nhau tại $C$ nên $AC = MC$

$MD$ và $BD$ là hai tiếp tuyến cắt nhau tại $D$ nên $BD = MD$

Suy ra $AC.BD = MC.MD\left( 3 \right)$

Xét tam giác $OCD$ vuông tại O có $OM$ là đường cao:

$MC.MD = O{M^2} = {\left( {\frac{1}{2}AB} \right)^2} = \frac{1}{4}A{B^2}\left( 4 \right)$

Từ $\left( 3 \right)$ và $\left( 4 \right)$ suy ra: $AC.BD = \frac{1}{4}A{B^2}$

Hay $4.AC.BD = A{B^2}\,\,$(đpcm)

c) Lấy $N$ là trung điểm của $OC$

Xét $\Delta OCD$ vuông tại $O$ có $ON$ là trung tuyến nên: $NO = NC = ND\left( * \right)$

$\Rightarrow$N là tâm đường tròn ngoại tiếp $\Delta OCD$(a)

Từ (*) suy ra tam giác $NCO$ cân tại $N$

$\Rightarrow \widehat {NCO} = \widehat {NOC}$ mà $\widehat {NCO} = \widehat {AOC}$(tính chất hai tiếp tuyến cắt nhau)

$\Rightarrow \widehat {AOC} = \widehat {NCO}$

Ta có:

$\widehat {NOA} = \widehat {NOC} + \widehat {AOC}$

$= \widehat {ACO} + \widehat {AOC} = {90^0}$(Do $\Delta OCD$ vuông tại A)

$\Rightarrow NO \bot AB$(b)

Từ (a) và (b) suy ra AB là tiếp tuyến của đường tròn ngoại tiếp $\Delta OCD$

Bài 5:

Gọi: Ngọn hải đăng là điểm A, chân là điểm B

Điểm mà người đó nhìn thấy lần thứ nhất và thứ hai lần lượt là: C và D

Ta có:

$\widehat {BAD} = {90^0} - {30^0} = {60^0}$

$\widehat {BAC} = {90^0} - {20^0} = {70^0}$

$\begin{array}{l}\tan \widehat {BAC} = \frac{{BC}}{{AB}}\\ \Rightarrow BC = AB.\tan \widehat {BAC}\\ \Rightarrow BC = 100.\tan {70^0} = 275\left( m \right)\end{array}$

$\begin{array}{l}\tan \widehat {BAD} = \frac{{BD}}{{AB}}\\ \Rightarrow BD = AB.\tan \widehat {BAD}\\ \Rightarrow BD = 100.\tan {60^0} = 173\left( m \right)\end{array}$

Ta có $BC - BD = 275 - 173 = 102\left( m \right)$

Vậy thuyền đã đi được $102\,$ mét giữa hai lần quan sát.

b)

Biến đổi giả thiết bài toán thành:

$xy > 2020x + 2021y \Leftrightarrow 1 > \frac{{2020}}{y} + \frac{{2021}}{x}$

Do đó, ta có:

$x + y = \left( {x + y} \right).1 > \left( {x + y} \right)\left( {\frac{{2021}}{x} + \frac{{2020}}{y}} \right) \ge {\left( {\sqrt {x.\frac{{2021}}{x}}  + \sqrt {y.\frac{{2020}}{y}} } \right)^2}$(Bất đẳng thức Bunnhiacopxki)

$\Rightarrow x + y > {\left( {\sqrt {2020}  + \sqrt {2021} } \right)^2}$

Vậy ta có điều phải chứng minh.