Giải đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Cầu Giấy — Không quảng cáo

Đề bài

Bài 1  (2,0 điểm):

Cho biểu thức $A = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} - \dfrac{6}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}$  và $B = \dfrac{2}{{\sqrt x  - 2}}$ với $x \ge 0$ và $x \ne 4.$

1) Tính giá trị biểu thức $B$ khi $x = 16.$

2) Biết $P = A + B.$ Chứng minh $P = \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}}$

3) Tìm $x$ để $P > \dfrac{3}{2}$

Bài 2 (2,0 điểm):

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Một đoàn xe vận tải dự định sử dụng một số xe cùng loại để chuyên chở 90 tấn thiết bị y tế. Để đáp ứng kịp nhu cầu phục vụ công tác phòng chống dịch Covid – 19 đoàn được bổ sung thêm 5 chiếc xe cùng loại. Do đó mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn. Biết khối lượng hàng mỗi xe chuyên chở như nhau, hỏi ban đầu đoàn xe có bao nhiêu chiếc?

2) Một lọ thuốc hình trụ có chiều cao 10cm và bán kính đáy 5cm. Nhà sản xuất phủ kín mặt xung quanh của lọ thuốc bằng giấy in các thông tin về loại thuốc ấy. Hãy tính diện tích giấy cần dùng của lọ thuốc đó (cho biết độ dày của giấy in và lọ thuốc không đáng kể)?

Bài 3 (2,0 điểm):

1) Giải hệ phương trình $\left\{ \begin{array}{l}x + \sqrt {2y - 5}  = 12\\2x - \sqrt {2y - 5}  = 3\end{array} \right.$

2) Cho phương trình ${x^2} - 2x + m - 3 = 0$ ($m$ là tham số)

a. Giải phương trình khi $m =  - 5$

b. Tìm $m$ để phương trình có hai nghiệm phân biệt ${x_1};{x_2}$ thỏa mãn điều kiện ${x_1} = 3{x_2}.$

Bài 4 (3,5 điểm): C

Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $\left( {O;R} \right)$. Các đường cao $BD$ và $CE$ cắt nhau tại $H.$

1) Chứng minh $ADHE$ là tứ giác nội tiếp

2) Kẻ đường kính $AK.$ Chứng minh $CK//BH$ và tứ giác $BHCK$ là hình bình hành

3) Gọi $I$ là trung điểm của $BC,G$ là giao điểm của $AI$ và $OH.$

a. Chứng minh $G$ là trọng tâm $\Delta AHK$

b. Cho $B,C$ cố định, khi $A$ di động trên cung lớn $BC$ sao cho $\Delta ABC$ có 3 góc nhọn thì $G$ chuyển động trên đường nào? Tại sao?

Bài 5 (3 điểm):

Cho các số thực $x,y$ thỏa mãn ${x^2} + {y^2} - 4x + 3 = 0$. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức $A = {x^2} + {y^2}.$

HẾT

LG bài 1

Phương pháp giải:

a) Thay $x = 16$ vào $B$ rồi tính toán

b) Quy đồng và rút gọn các biểu thức

c) Đưa về giải bất phương trình, kết hợp điều kiện để có kết quả đúng.

Lời giải chi tiết:

Cho biểu thức $A = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} - \dfrac{6}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}$ và $B = \dfrac{2}{{\sqrt x  - 2}}$ với $x \ge 0$ và $x \ne 4.$

1) Tính giá trị biểu thức $B$ khi $x = 16.$

Thay $x = 16$(thỏa mãn điều kiện) vào biểu thức $B$ ta được:

$B = \dfrac{2}{{\sqrt {16}  - 2}}$ $= \dfrac{2}{{4 - 2}} = \dfrac{2}{2} = 1$

Vậy với $x = 16$ thì $B = 1.$

2) Biết $P = A + B.$ Chứng minh $P = \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}}$

Với $x \ge 0;x \ne 4$ ta có:

$P = A + B$ $= \dfrac{{\sqrt x }}{{\sqrt x  + 1}} - \dfrac{6}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} + \dfrac{2}{{\sqrt x  - 2}}$

$= \dfrac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} - \dfrac{6}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}$ $+ \dfrac{{2\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}$

$= \dfrac{{\sqrt x \left( {\sqrt x  - 2} \right) - 6 + 2\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}$

$\begin{array}{l} = \dfrac{{x - 2\sqrt x  - 6 + 2\sqrt x  + 2}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{x - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}}\end{array}$

Vậy $P = \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}}$  với $x \ge 0,x \ne 4.$

3) Tìm $x$ để $P > \dfrac{3}{2}$

Với $x \ge 0,x \ne 4$, ta có: $P > \dfrac{3}{2} \Leftrightarrow \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}} > \dfrac{3}{2}$

$\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}} - \dfrac{3}{2} > 0\\ \Leftrightarrow \dfrac{{2\sqrt x  + 4 - 3\sqrt x  - 3}}{{\sqrt x  + 1}} > 0\\ \Leftrightarrow \dfrac{{1 - \sqrt x }}{{\sqrt x  + 1}} > 0\end{array}$

Mà $\sqrt x  + 1 > 0$ với mọi $x \ge 0;x \ne 4$

Nên $1 - \sqrt x  > 0 \Leftrightarrow \sqrt x  < 1$ $\Leftrightarrow x < 1$

Kết hợp điều kiện $x \ge 0;x \ne 4$ ta có: $0 \le x < 1$

Vậy với $0 \le x < 1$ thì $P > \dfrac{3}{2}.$

LG bài 2

Phương pháp giải:

1) Gọi số xe ban đầu là $x$ chiếc rồi giải bài toán bằng cách lập phương trình theo ẩn $x.$

2) Diện tích xung quanh của hình trụ có bán kính đáy $R$ và chiều cao $h$ là ${S_{xq}} = 2\pi Rh$

Lời giải chi tiết:

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Một đoàn xe vận tải dự định sử dụng một số xe cùng loại để chuyên chở 90 tấn thiết bị y tế. Để đáp ứng kịp nhu cầu phục vụ công tác phòng chống dịch Covid – 19 đoàn được bổ sung thêm 5 chiếc xe cùng loại. Do đó mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn. Biết khối lượng hàng mỗi xe chuyên chở như nhau, hỏi ban đầu đoàn xe có bao nhiêu chiếc?

Gọi số xe ban đầu của đoàn là $x$ (xe) $\left( {x \in {\mathbb{N}^*}} \right)$

Theo dự định, mỗi xe chở số thiết bị y tế là: $\dfrac{{90}}{x}$ (tấn)

Thực tế được bổ sung thêm 5 xe nên tổng số xe là $x + 5$ xe

Khi đó mỗi xe phải chở số thiết bị y tế là: $\dfrac{{90}}{{x + 5}}$ (tấn)

Vì mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn nên ta có phương trình:

$\begin{array}{l}\dfrac{{90}}{x} - \dfrac{{90}}{{x + 5}} = 0,2\\ \Leftrightarrow \dfrac{{90\left( {x + 5} \right) - 90x}}{{x\left( {x + 5} \right)}} = 0,2\\ \Rightarrow 90\left( {x + 5} \right) - 90x = 0,2x\left( {x + 5} \right)\\ \Leftrightarrow 90x + 450 - 90x = 0,2{x^2} + x\\ \Leftrightarrow 0,2{x^2} + x - 450 = 0\\ \Leftrightarrow {x^2} + 5x - 2250 = 0\\ \Leftrightarrow {x^2} - 45x + 50x - 2250 = 0\\ \Leftrightarrow x\left( {x - 45} \right) + 50\left( {x - 45} \right) = 0\\ \Leftrightarrow \left( {x - 45} \right)\left( {x + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 45 = 0\\x + 50 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 45\left( {tm} \right)\\x =  - 50\left( {ktm} \right)\end{array} \right.\end{array}$

Vậy ban đầu đoàn có 45 xe.

2) Một lọ thuốc hình trụ có chiều cao 10cm và bán kính đáy 5cm. Nhà sản xuất phủ kín mặt xung quanh của lọ thuốc bằng giấy in các thông tin về loại thuốc ấy. Hãy tính diện tích giấy cần dùng của lọ thuốc đó (cho biết độ dày của giấy in và lọ thuốc không đáng kể)?

Diện tích giấy cần dùng là diện tích xung quanh của hình trụ có chiều cao 10cm và bán kính đáy 5cm.

Ta có: ${S_{xq}} = 2\pi Rh$ $= 2\pi .5.10 = 100\pi$$\approx 314c{m^2}$

LG bài 3

Phương pháp giải:

1) Đặt ẩn phụ rồi giải hệ phương trình bằng phương pháp cộng đại số

2) Sử dụng công thức nghiệm và hệ thức Vi-ét

Lời giải chi tiết:

1) Giải hệ phương trình $\left\{ \begin{array}{l}x + \sqrt {2y - 5}  = 12\\2x - \sqrt {2y - 5}  = 3\end{array} \right.$

ĐK: $y \ge \dfrac{5}{2}$

Đặt $u = \sqrt {2y - 5} \left( {u \ge 0} \right)$, ta có hệ phương trình:

$\begin{array}{l}\left\{ \begin{array}{l}x + u = 12\\2x - u = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x = 15\\x + u = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5\\5 + u = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 5\\u = 7\end{array} \right.\end{array}$

Thay lại cách đặt, ta được: $u = 7 \Rightarrow \sqrt {2y - 5}  = 7$

$\Leftrightarrow 2y - 5 = 49$ $\Leftrightarrow 2y = 54 \Leftrightarrow y = 27$ (thỏa mãn)

Vậy hệ phương trình có nghiệm $\left( {x;y} \right) = \left( {5;27} \right)$

2) Cho phương trình ${x^2} - 2x + m - 3 = 0$ ( $m$ là tham số)

a. Giải phương trình khi $m =  - 5$

Với $m =  - 5$ ta có phương trình ${x^2} - 2x - 8 = 0$

$\begin{array}{l} \Leftrightarrow {x^2} + 2x - 4x - 8 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - 4\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\x + 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - 2\end{array} \right.\end{array}$

Vậy phương trình có nghiệm $x = 4;x =  - 2.$

b. Tìm $m$ để phương trình có hai nghiệm phân biệt ${x_1};{x_2}$ thỏa mãn điều kiện ${x_1} = 3{x_2}.$

Ta có: $\Delta ' = {\left( { - 1} \right)^2} - \left( {m - 3} \right)$ $= 1 - m + 3 = 4 - m$

Để phương trình có hai nghiệm phân biệt ${x_1};{x_2}$ thì $\left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\4 - m > 0\end{array} \right.$$\Leftrightarrow m < 4$

Theo hệ thức Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 3\end{array} \right.$

Theo đề bài ${x_1} = 3{x_2}$ nên ta có hệ phương trình:

$\begin{array}{l}\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1} = 3{x_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x_2} + {x_2} = 2\\{x_1} = 3{x_2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{x_2} = 2\\{x_2} = 3{x_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \dfrac{1}{2}\\{x_1} = \dfrac{3}{2}\end{array} \right.\end{array}$

Thay ${x_2} = \dfrac{1}{2};{x_1} = \dfrac{3}{2}$ vào ${x_1}{x_2} = m - 3$ ta được:

$\begin{array}{l}\dfrac{1}{2}.\dfrac{3}{2} = m - 3\\ \Leftrightarrow m - 3 = \dfrac{3}{4}\\ \Leftrightarrow m = 3 + \dfrac{3}{4}\end{array}$

$\Leftrightarrow m = \dfrac{{15}}{4}$ (thỏa mãn)

Vậy $m = \dfrac{{15}}{4}$ thỏa mãn yêu cầu đề bài.

LG bài 4

Phương pháp giải:

1) Chứng minh tứ giác ADHE có hai góc đối có tổng số đo bằng ${180^0}$ .

2) Chứng minh $CK \bot AC,BH \bot AC$, từ đó suy ra $CK//BH$.

Chứng minh tứ giác BHCK có hai cặp cạnh đối song song.

3) a) Chứng minh G là giao điểm hai đường trung tuyến trong tam giác AHK.

b) Kẻ GM//OA $\left( {M \in OI} \right)$, chứng minh $MG = \dfrac{1}{3}OA$ không đổi.

Lời giải chi tiết:

Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $\left( {O;R} \right)$ . Các đường cao $BD$ và $CE$ cắt nhau tại $H.$

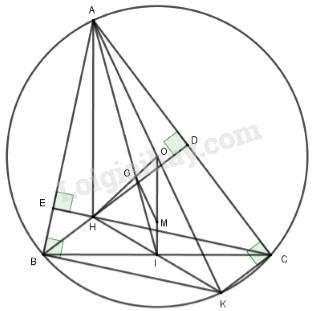
1) Chứng minh $ADHE$ là tứ giác nội tiếp

Ta có: $BD \bot AC$ nên $\widehat {ADB} = {90^0}$

$CE \bot AB$ nên $\widehat {AEC} = {90^0}$

Tứ giác ADHE có: $\widehat {AEH} + \widehat {ADH}$ $= {90^0} + {90^0} = {180^0}$

Do đó ADHE là tứ giác nội tiếp (Tứ giác có hai góc đối có tổng bằng ${180^0}$ là tứ giác nội tiếp) (đpcm).

2) Kẻ đường kính $AK.$ Chứng minh $CK//BH$ và tứ giác $BHCK$ là hình bình hành

Ta có: $BD \bot AC \Rightarrow BH \bot AC$ (1)

AK là đường kính nên $\widehat {KCA} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow CK \bot AC$ (2)

Từ (1) và (2) suy ra $BH//CK$ (cùng vuông góc với $AC$) (đpcm).

Lại có,

AK là đường kính nên $\widehat {ABK} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow BK \bot AB$

Mà $CE \bot AB \Rightarrow CH \bot AB$

Do đó $BK//CH$ (cùng vuông góc với $AB$)

Tứ giác BHCK có $BH//KC,BK//CH$ nên là hình bình hành (tứ giác có hai cặp đối song song là hình bình hành). (đpcm)

3) Gọi $I$ là trung điểm của $BC,G$ là giao điểm của $AI$ và $OH.$

a. Chứng minh $G$ là trọng tâm $\Delta AHK$

Tứ giác BHCK là hình bình hành (cmt) nên I là trung điểm BC cũng là trung điểm của HK (tính chất)

AK là đường kính nên O là trung điểm của AK.

Xét tam giác AHK có G là giao điểm hai đường trung tuyến AI và HO nên G là trọng tâm tam giác. (đpcm)

b. Cho $B,C$ cố định, khi $A$ di động trên cung lớn $BC$ sao cho $\Delta ABC$ có 3 góc nhọn thì $G$ chuyển động trên đường nào? Tại sao?

Qua G kẻ đường thẳng song song với OA cắt OI tại M.

$GM//AO$ nên theo định lí Ta let ta có: $\dfrac{{MG}}{{OA}} = \dfrac{{IG}}{{IA}} = \dfrac{{IM}}{{IO}}$

Mà G là trọng tâm tam giác AHK nên $\dfrac{{AG}}{{AI}} = \dfrac{2}{3} \Rightarrow \dfrac{{IG}}{{IA}} = \dfrac{1}{3}$

Do đó $\dfrac{{MG}}{{OA}} = \dfrac{{IG}}{{IA}} = \dfrac{{IM}}{{IO}} = \dfrac{1}{3}$

Do B, C, O cố định nên I cố định và $\dfrac{{IM}}{{IO}} = \dfrac{1}{3}$ nên M cố định.

Lại có $\dfrac{{MG}}{{OA}} = \dfrac{1}{3} \Rightarrow MG = \dfrac{1}{3}OA$. Mà $OA = R$ không đổi.

Do đó G luôn cách M một khoảng $MG = \dfrac{1}{3}OA = \dfrac{1}{3}R$ không đổi.

Vậy G luôn di chuyển trên đường tròn tâm M bán kính $R' = \dfrac{R}{3}$.

LG bài 5

Phương pháp giải:

- Từ đẳng thức bài cho rút ra ${x^2} - 4x + 3 =  - {y^2}$, đánh giá điều kiện của $x$.

- Biểu diễn A theo biến $x$ và chú ý từ điều kiện tìm được ở trên suy ra A.

Lời giải chi tiết:

Ta có:

${x^2} + {y^2} - 4x + 3 = 0$$\Leftrightarrow {x^2} - 4x + 3 =  - {y^2}$

Do ${y^2} \ge 0,\forall y \in \mathbb{R}$ nên $- {y^2} \le 0,\forall y \in \mathbb{R}$

$\begin{array}{l} \Rightarrow {x^2} - 4x + 3 \le 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) \le 0\,\,\left( * \right)\end{array}$

TH1: $\left\{ \begin{array}{l}x - 1 \ge 0\\x - 3 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \le 3\end{array} \right.$ $\Leftrightarrow 1 \le x \le 3$

TH2: $\left\{ \begin{array}{l}x - 1 \le 0\\x - 3 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\x \ge 3\end{array} \right.\left( {VN} \right)$

Do đó $\left( * \right) \Leftrightarrow 1 \le x \le 3$.

Lại có, ${x^2} + {y^2} - 4x + 3 = 0$ $\Leftrightarrow {y^2} =  - {x^2} + 4x - 3$

Do đó

$\begin{array}{l}A = {x^2} + {y^2}\\ = {x^2} + \left( { - {x^2} + 4x - 3} \right)\\ = {x^2} - {x^2} + 4x - 3\\ = 4x - 3\\ \Rightarrow A = 4x - 3\end{array}$

Từ $1 \le x \le 3$ suy ra:

$\begin{array}{l}4 \le 4x \le 12\\ \Rightarrow 4 - 3 \le 4x - 3 \le 12 - 3\\ \Rightarrow 1 \le A \le 9\end{array}$

Vậy GTNN của A là $A = 1$ khi $x = 1,y = 0$.

GTLN của A là $A = 9$ khi $x = 3,y = 0$.

HẾT