Giải đề thi học kì 1 toán lớp 9 năm 2019 - 2020 sở giáo dục Vĩnh Phúc
Tải vềGiải chi tiết đề thi học kì 1 môn toán lớp 9 năm 2019 - 2020 sở giáo dục Vĩnh Phúc với cách giải nhanh và chú ý quan trọng
I. PHẦN TRẮC NGHIỆM: (3,0 điểm) Hãy viết vào tờ giấy thi chữ cái in hoa trước đáp án đúng.
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {x - 8} \) là
A. \(x \ge 8.\) B. \(x > 8.\)
C. \(x < 8.\) D. \(x \le 8.\)
Câu 2. Đường thẳng nào sau đây không song song với đường thẳng \(y = 7x + 3?\)
A. \(y = 7x.\) B. \(y = 4 - 7x.\)
C. \(y = 7x + 1.\) D. \(y = - 1 + 7x.\)
Câu 3. Giá trị của biểu thức \(\sqrt {0,{{04.30}^2}} \) bằng
A .\(6.\) B. \(0,12.\)
C. \(12.\) D. \(0,24.\)
Câu 4. Cho tam giác \(ABC\) vuông tại \(A,\) biết \(AB = 6cm,\) \(AC = 8cm.\) Khi đó độ dài đoạn thẳng \(BC\) bằng
A. \(10cm.\) B. \(\sqrt {14} cm.\)
C. \(\sqrt 2 cm.\) D. \(14cm.\)
Câu 5. Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Hệ thức nào trong các hệ thức sau là đúng?
A. \(AH.HB = CB.CA.\)
B. \(A{B^2} = CH.BH.\)
C. \(A{C^2} = BH.BC.\)
D. \(AH.BC = AB.AC.\)
Câu 6. Cho tam giác \(MNP\) vuông ở \(M,\,MN = 4a;\) \(MP = 3a.\) Khi đó, \(\tan P\) bằng
A. \(\dfrac{3}{4}.\) B. \(\dfrac{4}{3}.\)
C. \(\dfrac{3}{5}.\) D. \(\dfrac{4}{5}.\)
II. PHẦN TỰ LUẬN (7 điểm).
Câu 7: (1,5 điểm)
a) Tính giá trị của biểu thức : \(\sqrt {20} - 3\sqrt 5 + 2\sqrt {45} .\)
b) Tìm \(x,\) biết : \(\sqrt {x - 1} + \sqrt {4x - 4} = 9.\)
Câu 8: (1,0 điểm) Cho hàm số bậc nhất : \(y = \left( {k - 2} \right)x + {k^2} - 2k;\) ( \(k\) là tham số)
a) Vẽ đồ thị hàm số khi \(k = 1.\)
b) Tìm \(k\) để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2.\)
Câu 9: (1,5 điểm) Cho biểu thức \(P = \left( {\dfrac{1}{{\sqrt a + 1}} - \dfrac{1}{{a + \sqrt a }}} \right):\dfrac{{\sqrt a - 1}}{{a + 2\sqrt a + 1}}\) với \(a > 0\) và \(a \ne 1\)
a) Rút gọn \(P.\)
b) Tìm \(a\) để \(P\) có giá trị bằng \(2.\)
Câu 10: (2,5 điểm) Cho \(\left( {O;R} \right),\) lấy điểm \(A\) cách \(O\) một khoảng bằng \(2R.\) Kẻ các tiếp tuyến \(AB\) và \(AC\) với đường tròn (\(B,C\) là các tiếp điểm). Đường thẳng qua \(O\) và vuông góc với \(OB\) cắt \(AC\) tại \(K.\)
a) Tính độ dài đoạn thẳng \(AB\) theo \(R.\)
b) Tính số đo góc \(BOA.\)
c) Chứng minh tam giác \(OAK\) cân tại \(K.\)
Câu 11: (0,5 điểm) Cho \(a,\,\,b,\,\,c\) là các số không âm thỏa mãn :
\(\sqrt a + \sqrt b + \sqrt c = \sqrt 3 \) và \(\sqrt {\left( {a + 2b} \right)\left( {a + 2c} \right)} + \sqrt {\left( {b + 2a} \right)\left( {b + 2c} \right)} + \sqrt {\left( {c + 2a} \right)\left( {c + 2b} \right)} = 3.\)
Tính giá trị của biểu thức \(M = {\left( {2\sqrt a + 3\sqrt b - 4\sqrt c } \right)^2}.\)
HẾT
(Thí sinh không sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I: TRẮC NGHIỆM
|
1.A |
2.B |
3.A |
4.A |
5.D |
6.B |
Câu 1 (NB):
Phương pháp:
Biểu thức \(\sqrt A \) xác định khi \(A \ge 0\)
Cách giải:
Ta có: \(\sqrt {x - 8} \) xác định khi \(x - 8 \ge 0 \Leftrightarrow x \ge 8\)
Chọn A
Câu 2 (NB):
Phương pháp:
Hai đường thẳng \(\left( d \right):y = ax + b,\left( {d'} \right):y = a'x + b'\)
+) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)
+) Cắt nhau khi \(a \ne a'\)
Cách giải:
Đường thẳng \(y = 7x + 3\) và đường thẳng \(y = 4 - 7x\) có \(7 \ne - 7\) nên hai đường thẳng này cắt nhau tức là chúng không song song.
Chọn B
Câu 3 (TH):
Phương pháp:
Sử dụng \(\sqrt {{A^2}} = \left| A \right|\) và \(\sqrt {A.B} = \sqrt A .\sqrt B \,\left( {A,B \ge 0} \right)\)
Cách giải:
Ta có: \(\sqrt {0,{{04.30}^2}} = \sqrt {0,{2^2}{{.30}^2}} \\= \sqrt {0,{2^2}} .\sqrt {{{30}^2}} \) \( = 0,2.30 = 6\)
Chọn A
Câu 4 (TH):
Phương pháp:
Sử dụng định lý Pytago để tính cạnh \(BC.\)
Cách giải:
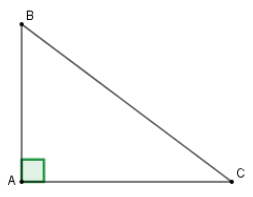
Xét tam giác \(ABC\) vuông tại \(A\), theo định lý Pytago ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10cm\)
Chọn A
Câu 5 (NB):
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông
Cách giải:
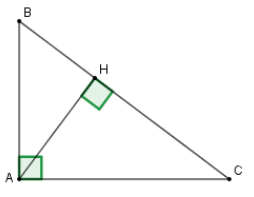
Xét tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH.\) Theo hệ thức lượng trong tam giác vuông ta có: \(AH.BC = AB.AC\) nên D đúng.
Chọn D
Câu 6 (TH):
Phương pháp:
Sử dụng tỉ số lượng giác của góc nhọn
Cách giải:
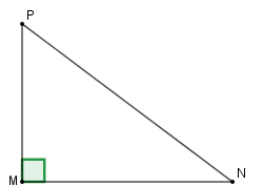
Xét tam giác \(MNP\) vuông tại \(M,\) theo định nghĩa tỉ số lượng giác của góc nhọn ta có:
\(\tan P = \dfrac{{MN}}{{MP}} = \dfrac{{4a}}{{3a}} = \dfrac{4}{3}.\)
Chọn B
PHẦN II: TỰ LUẬN
Câu 7 (VD)
Phương pháp:
a) \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \,\,\left( {B \ge 0} \right)\)
b) Sử dụng \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \,\,\left( {B \ge 0} \right)\) để đưa về dạng \(\sqrt A = m\left( {m \ge 0} \right) \Leftrightarrow A = {m^2}\,\,\left( {A \ge 0} \right)\)
Cách giải:
a) Tính giá trị của biểu thức : \(\sqrt {20} - 3\sqrt 5 + 2\sqrt {45} .\)
Ta có: \(\sqrt {20} - 3\sqrt 5 + 2\sqrt {45} \)\( = \sqrt {4.5} - 3\sqrt 5 + 2\sqrt {9.5} \) \( \\= 2\sqrt 5 - 3\sqrt 5 + 2.3\sqrt 5 \\= 2\sqrt 5 - 3\sqrt 5 + 6\sqrt 5 = 5\sqrt 5 \)
b) Tìm \(x,\) biết : \(\sqrt {x - 1} + \sqrt {4x - 4} = 9.\)
Điều kiện: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Ta có: \(\sqrt {x - 1} + \sqrt {4x - 4} = 9.\)
\(\begin{array}{l} \Leftrightarrow \sqrt {x - 1} + \sqrt {4\left( {x - 1} \right)} = 9\\ \Leftrightarrow \sqrt {x - 1} + 2\sqrt {x - 1} = 9\\ \Leftrightarrow 3\sqrt {x - 1} = 9\\ \Leftrightarrow \sqrt {x - 1} = 3\\ \Leftrightarrow x - 1 = 9\\ \Leftrightarrow x = 10\left( {tm} \right)\end{array}\)
Vậy \(x = 10.\)
Câu 8 (VD)
Phương pháp:
a) Thay \(k = 1\) vào hàm số rồi vẽ đồ thị hàm số thu được.
b) Xác định tọa độ giao điểm. Thay tọa độ đó vào hàm số, từ đó ta tìm được \(m.\)
Cách giải:
Cho hàm số bậc nhất : \(y = \left( {k - 2} \right)x + {k^2} - 2k;\) ( \(k\) là tham số)
a) Vẽ đồ thị hàm số khi \(k = 1.\)
Thay \(k = 1\) vào hàm số ta được: \(y = \left( {1 - 2} \right)x + {1^2} - 2.1 \Leftrightarrow y = - x - 1\)
Với \(x = 0 \Rightarrow y = - 1\)
\(x = - 1 \Rightarrow y = 0\)
Đồ thị hàm số \(y = - x - 1\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0; - 1} \right),\left( { - 1;0} \right)\)
Hình vẽ:
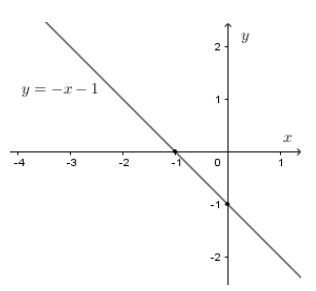
b) Tìm \(k\) để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2.\)
Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2\) nên \(k - 2 \ne 0 \Leftrightarrow k \ne 2\) và tọa độ giao điểm của đồ thị hàm số với trục hoành là \(\left( {2;0} \right)\)
Thay \(x = 2;y = 0\) vào hàm số đã cho ta được:
\(\begin{array}{l}0 = \left( {k - 2} \right).2 + {k^2} - 2k\\ \Leftrightarrow {k^2} - 4 = 0\\ \Leftrightarrow {k^2} = 4\\ \Leftrightarrow \left[ \begin{array}{l}k = 2\left( L \right)\\k = - 2\left( N \right)\end{array} \right.\end{array}\)
Vậy \(k = - 2.\)
Câu 9 (VD)
Phương pháp:
a) Qui đồng mẫu các phân thức, cộng trừ các phân thức sau đó rút gọn phân thức thu được
b) Cho \(P = 2\) rồi qui đồng hai vế để tìm \(a.\)
Cách giải:
Cho biểu thức \(P = \left( {\dfrac{1}{{\sqrt a + 1}} - \dfrac{1}{{a + \sqrt a }}} \right):\dfrac{{\sqrt a - 1}}{{a + 2\sqrt a + 1}}\) với \(a > 0\) và \(a \ne 1\)
a) Rút gọn \(P.\)
Với \(a > 0;a \ne 1\) ta có:
\(\begin{array}{l}P = \left( {\dfrac{1}{{\sqrt a + 1}} - \dfrac{1}{{\sqrt a \left( {\sqrt a + 1} \right)}}} \right):\dfrac{{\sqrt a - 1}}{{{{\left( {\sqrt a + 1} \right)}^2}}}\\ = \dfrac{{\sqrt a - 1}}{{\sqrt a \left( {\sqrt a + 1} \right)}}.\dfrac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{\sqrt a - 1}}\\ = \dfrac{{\sqrt a + 1}}{{\sqrt a }}\end{array}\)
Vậy \(P = \dfrac{{\sqrt a + 1}}{{\sqrt a }}\) với \(a > 0;a \ne 1\)
b) Tìm \(a\) để \(P\) có giá trị bằng \(2.\)
Ta có: \(P = \dfrac{{\sqrt a + 1}}{{\sqrt a }}\) với \(a > 0;a \ne 1\)
Để \(P = 2\) thì \(\dfrac{{\sqrt a + 1}}{{\sqrt a }} = 2 \Rightarrow \sqrt a + 1 = 2\sqrt a \\ \Leftrightarrow \sqrt a = 1 \Leftrightarrow a = 1\left( {ktm} \right)\)
Vậy không có giá trị nào của \(a\) thỏa mãn điều kiện đề bài.
Câu 10 (VD):
Phương pháp:
a) Sử dụng định lý Pytago
b) Sử dụng tỉ số lượng giác của góc nhọn
c) Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất hai đường thẳng song song để chỉ ra tam giác \(OKA\) có hai góc \(\widehat {OAK},\,\widehat {KOA}\) bằng nhau.
Cách giải:
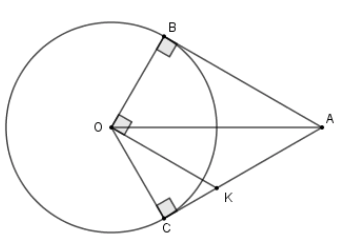
a) Tính độ dài đoạn thẳng \(AB\) theo \(R.\)
Vì \(AB\) là tiếp tuyến của \(\left( {O;R} \right)\) nên \(AB \bot OB\) tại \(B\)
Xét tam giác \(OAB\) vuông tại \(B\) có \(OA = 2R\left( {gt} \right),OB = R\). Theo định lý Pytago ta có:
\(A{B^2} = O{A^2} - O{B^2} = 4{R^2} - {R^2} = 3{R^2}\) nên \(AB = R\sqrt 3 .\)
b) Tính số đo góc \(BOA.\)
Xét tam giác \(OAB\) vuông tại \(B\) có \(OA = 2R\left( {gt} \right),OB = R\) nên theo tỉ số lượng giác của góc nhọn ta có: \(\cos \widehat {BOA} = \dfrac{{OB}}{{OA}} = \dfrac{R}{{2R}} = \dfrac{1}{2}\), suy ra \(\widehat {BOA} = {60^0}.\)
c) Chứng minh tam giác \(OAK\) cân tại \(K.\)
Xét đường tròn \(\left( O \right)\) có \(AB,AC\) là hai tiếp tuyến cắt nhau tại \(A\) nên \(AO\) là phân giác \(\widehat {BAC}\) (tính chất) hay \(\widehat {BAO} = \widehat {OAK}\) (1)
Lại có \(AB \bot OB\left( {cmt} \right)\) và \(OK \bot OB\left( {gt} \right)\) suy ra \(OK//AB\)
Do đó: \(\widehat {BOA} = \widehat {AOK}\) (2) (hai góc ở vị trí so le trong)
Từ (1) và (2) ta có \(\widehat {KOA} = \widehat {KAO}\,\,\left( { = \widehat {BAO}} \right)\) suy ra tam giác \(OKA\) cân tại \(K\) (đpcm)
Câu 11 (VDC): (fb: Thầy Hoang Kien)
Phương pháp:
Áp dụng bất đẳng thức Cô-si cho hai số không âm \(a,b\) ta có: \(a + b \ge 2\sqrt {ab} \)
Dấu = xảy ra khi \(a = b.\)
Sử dụng các hằng đẳng thức: \({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2},\) \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2} + 2\left( {xy + xz + yz} \right)\)
Cách giải:
Theo bất đẳng thức Cô-si ta có: \(b + c \ge 2\sqrt {bc} ,\,a + c \ge 2\sqrt {ac} ,\,a + b \ge 2\sqrt {ab} \)
Xét \(\left( {a + 2b} \right)\left( {a + 2c} \right) = {a^2} + 2ac + 2ab + 4bc\) \( = {a^2} + 2a\left( {b + c} \right) + 4bc \ge {a^2} + 2a.2\sqrt {bc} + 4bc\)
\( \Leftrightarrow \left( {a + 2b} \right)\left( {a + 2c} \right) \ge {a^2} + 4a\sqrt {bc} + 4bc\) hay \(\left( {a + 2b} \right)\left( {a + 2c} \right) \ge {\left( {a + 2\sqrt {bc} } \right)^2}\)
\( \Rightarrow \sqrt {\left( {a + 2b} \right)\left( {a + 2c} \right)} \ge a + 2\sqrt {bc} \)
Tương tự ta có: \(\sqrt {\left( {b + 2a} \right)\left( {b + 2c} \right)} \ge b + 2\sqrt {ac} \)
\(\sqrt {\left( {c + 2a} \right)\left( {c + 2b} \right)} \ge c + 2\sqrt {ab} \)
Suy ra \(\sqrt {\left( {a + 2b} \right)\left( {a + 2c} \right)} + \sqrt {\left( {b + 2a} \right)\left( {b + 2c} \right)} + \sqrt {\left( {c + 2a} \right)\left( {c + 2b} \right)} \)\( \ge a + b + c + 2\left( {\sqrt {ab} + \sqrt {ac} + \sqrt {bc} } \right)\)
Hay \(3 \ge {\left( {\sqrt a + \sqrt b + \sqrt c } \right)^2} \Leftrightarrow 3 \ge 3\)
Dấu xảy ra \( \Leftrightarrow a = b = c = \dfrac{1}{3}.\)
Thay \(a = b = c = \dfrac{1}{3}\) vào biểu thức \(M\) ta có:
\(M = {\left( {2 \cdot \sqrt {\dfrac{1}{3}} + 3 \cdot \sqrt {\dfrac{1}{3}} - 4\sqrt {\dfrac{1}{3}} } \right)^2} \\= {\left( {\sqrt {\dfrac{1}{3}} } \right)^2} = \dfrac{1}{3}\)