Đề thi học kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Tân Phú
Tải vềGiải chi tiết đề thi học kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Tân Phú với cách giải nhanh và chú ý quan trọng
Bài 1: (3 điểm) Tính
a) \(4\sqrt 5 + \dfrac{3}{5}\sqrt {125} - \dfrac{1}{3}\sqrt {45} \)
b) \(\sqrt {28 - 10\sqrt 3 } + \left( {2\sqrt 3 + 1} \right)\sqrt 3 \)
c) \(\dfrac{{\sqrt {54} + \sqrt 2 }}{{\sqrt 3 + 1}} + \dfrac{4}{{\sqrt 6 + \sqrt 2 }}\)
Bài 2: (0,75 điểm) Giải phương trình : \(\sqrt {9 - 2x} = \sqrt {{x^2} + 9} .\)
Bài 3: (1,5 điểm) a) Vẽ đồ thị \(\left( {{d_1}} \right)\) của hàm số \(y = 3x - 2\) và đồ thị \(\left( {{d_2}} \right)\) của hàm số \(y = - 2x + 3\) trên cùng hệ trục tọa độ.
b) Tìm hệ số \(a,\,b\) của đường thẳng \(\left( {{d_3}} \right):y = ax + b,\) biết \(\left( {{d_3}} \right)\) song song với \(\left( {d{ _1}} \right)\) và cắt đường thẳng \(\left( {{d_2}} \right)\) tại điểm có hoành độ bằng \(2.\)
Bài 4: (1,0 điểm) Nhà An cách trường khoảng \(3km\). Trường An tổ chức học tập trải nghiệm cho khối \(9\) vào cuối học kỳ \(I.\) An rời nhà lúc \(6\) giờ sáng và xe du lịch đến đón học sinh để xuất phát từ trường đi đến Đà Lạt với vận tốc trung bình \(45km/h.\)
a) Viết công thức biểu diễn quãng đường \(y\left( {km} \right)\) từ nhà An đến Đà Lạt theo thời gian \(x\) (giờ) mà xe di chuyển từ trường đến Đà Lạt.
b) Biết khoảng cách từ nhà An đến Đà Lạt khoảng \(318km\) và trên đường đi chuyến xe có nghỉ ngơi \(1\) giờ \(30\) phút. Tính thời điểm xe phải xuất phát từ trường để đến nơi vào lúc \(15\) giờ.
Bài 5: (0,75 điểm) Bác Ba gửi \(100\) triệu đồng vào ngân hàng với lãi suất \(7\% \) / năm. Sau hai năm, bác rút hết tiền ra. Hỏi bác Ba nhận được cả vốn và lãi là bao nhiêu tiền ? (biết tiền lãi được cộng dồn vào tiền vốn sau mỗi năm).
Bài 6: (2,5 điểm) Cho đường tròn \(\left( {O;R} \right)\) và điểm \(A\) nằm ở ngoài đường tròn sao cho \(OA < 2R.\) Vẽ các tiếp tuyến \(AB,\,AC\) (\(B,C\) là các tiếp điểm). \(BC\) cắt \(OA\) tại \(H\).
a) Chứng minh \(OA\) vuông góc với \(BC\) và \(OH.OA = {R^2}.\)
b) Vẽ cát tuyến \(ADE\) nằm bên trong góc \(BAO\) (\(AD\) nhỏ hơn \(AE\)). Vẽ \(OI\) vuông góc với \(DE\) tại \(I.\) Tia \(OI\) cắt \(AB\) tại \(F.\) Gọi \(G\) là giao điểm của \(DE\) với \(OB\) và \(Q\) là trung điểm của \(OG\). Tia \(FG\) cắt tia \(AO\) tại \(K.\) Chứng minh \(FK\) vuông góc với \(OA\) và \(QI\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(FIA.\)
c) Tiếp tuyến tại \(D\) của đường tròn \(\left( {O;R} \right)\) cắt tia \(OF\) tại \(M\). \(BH\) cắt \(AI\) tại \(N.\) Chứng minh \(\dfrac{2}{{BC}} = \dfrac{1}{{BN}} - \dfrac{1}{{BM}}.\)
Bài 7: (0,5 điểm) Các góc nhìn đến đỉnh núi có chiều cao là \(TN\) so với mực nước biển được đo từ hai đèn tín hiệu tại \(A\) và \(B\) trên mặt biển. Biết \(\widehat {TAB} = 29,7^\circ ,\,\widehat {TBN} = 41,2^\circ ,\,AB = 1500m.\) Hỏi chiều cao \(TN\) của ngọn núi khoảng bao nhiêu mét ? (làm tròn kết quả đến một chữ số thập phân.
HẾT
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1 (VD):
Phương pháp:
a) Sử dụng \(\sqrt {{A^2}B} = \left| A \right|.B\,\,\left( {B \ge 0} \right)\)
b) Sử dụng: \(\sqrt {{A^2}} = \left| A \right|\)
c) Khử mẫu biều thức lấy căn: \(\dfrac{1}{{\sqrt A + \sqrt B }} = \dfrac{{\sqrt A - \sqrt B }}{{A - B}}\,\,\left( {A,B \ge 0;\,A \ne B} \right)\)
Cách giải:
a) \(4\sqrt 5 + \dfrac{3}{5}\sqrt {125} - \dfrac{1}{3}\sqrt {45} \)
\( = 4\sqrt 5 + \dfrac{3}{5} \cdot \left( {5\sqrt 5 } \right) - \dfrac{1}{3}\left( {3\sqrt 5 } \right)\)
\( = \sqrt 5 \left( {4 + 3 - 1} \right)\)
\( = 6\sqrt 5 .\)
b) \(\sqrt {28 - 10\sqrt 3 } + \left( {2\sqrt 3 + 1} \right)\sqrt 3 \)
\( = \sqrt {25 - 2.5.\sqrt 3 + 3} + 2\sqrt 3 .\sqrt 3 + \sqrt 3 \)
\( = \sqrt {{{\left( {\sqrt {25} - \sqrt 3 } \right)}^2}} + 6 + \sqrt 3 \)
\( = \left( {5 - \sqrt 3 } \right) + 6 + \sqrt 3 = 11\)
c) \(\dfrac{{\sqrt {54} + \sqrt 2 }}{{\sqrt 3 + 1}} + \dfrac{4}{{\sqrt 6 + \sqrt 2 }}\)
\( = \dfrac{{\sqrt 2 \left( {\sqrt {27} + 1} \right)}}{{\sqrt 3 + 1}} + \dfrac{{4\left( {\sqrt 6 - \sqrt 2 } \right)}}{{\left( {\sqrt 6 + \sqrt 2 } \right)\left( {\sqrt 6 - \sqrt 2 } \right)}}\)
\( = \dfrac{{\sqrt 2 \left( {\sqrt 3 + 1} \right)\left( {3 - \sqrt 3 + 1} \right)}}{{\sqrt 3 + 1}} + \dfrac{{4\left( {\sqrt 6 - \sqrt 2 } \right)}}{{{{\left( {\sqrt 6 } \right)}^2} - {{\left( {\sqrt 2 } \right)}^2}}}\)
\( = \sqrt 2 \left( {4 - \sqrt 3 } \right) + \sqrt 6 - \sqrt 2 \)
\( = 4\sqrt 2 - \sqrt 6 + \sqrt 6 - \sqrt 2 = 3\sqrt 2 \)
Bài 2 (VD):
Phương pháp:
Giải phương trình dạng \(\sqrt {A\left( x \right)} = \sqrt {B\left( x \right)} \\ \Leftrightarrow \left\{ \begin{array}{l}A\left( x \right) \ge 0\\A\left( x \right) = B\left( x \right)\end{array} \right.\)
Cách giải:
\(\sqrt {9 - 2x} = \sqrt {{x^2} + 9} \)
\( \Leftrightarrow \left\{ \begin{array}{l}9 - 2x \ge 0\\9 - 2x = {x^2} + 9\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 2x \ge - 9\\{x^2} - 2x = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \le \dfrac{9}{2}\\x\left( {x + 2} \right) = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \le \dfrac{9}{2}\\\left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\end{array} \right.\)
Tập nghiệm \(S = \left\{ {0; - 2} \right\}.\)
Bài 3 (VD):
Phương pháp:
a) Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0;b} \right);\left( {\dfrac{{ - b}}{a};0} \right)\)
b) Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\)
+) Song song với nhau khi: \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)
+) Cắt nhau khi \(a \ne a'\)
Cách giải:
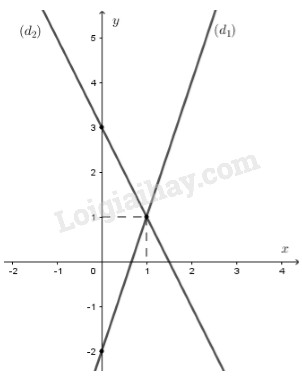
a) Vẽ đồ thị \(\left( {{d_1}} \right)\) của hàm số \(y = 3x - 2\) và đồ thị \(\left( {{d_2}} \right)\) của hàm số \(y = - 2x + 3\) trên cùng hệ trục tọa độ.
+) Đường thẳng \(\left( {{d_1}} \right):y = 3x - 2\)
Với \(x = 0 \Rightarrow y = 3.0 - 2 = - 2\)
Với \(x = 1 \Rightarrow y = 3.1 - 2 = 1\)
Vậy đường thẳng \(\left( {{d_1}} \right):y = 3x - 2\) đi qua hai điểm có tọa độ \(\left( {0; - 2} \right)\) và \(\left( {1;1} \right)\)
+) Đường thẳng \(\left( {{d_2}} \right):y = - 2x + 3\)
Với \(x = 0 \Rightarrow y = - 2.0 + 3 = 3\)
Với \(x = 1 \Rightarrow y = - 2.1 + 3 = 1\)
Vậy đường thẳng \(\left( {{d_2}} \right):y = - 2x + 3\) đi qua hai điểm có tọa độ \(\left( {0;3} \right)\) và \(\left( {1;1} \right)\)
Đồ thị hàm số:
b) Tìm hệ số \(a,\,b\) của đường thẳng \(\left( {{d_3}} \right):y = ax + b,\) biết \(\left( {{d_3}} \right)\) song song với \(\left( {d{ _1}} \right)\) và cắt đường thẳng \(\left( {{d_2}} \right)\) tại điểm có hoành độ bằng \(2.\)
Vì \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right):y = 3x - 2\)
Suy ra \(\left\{ \begin{array}{l}a = 3\\b \ne - 2\end{array} \right.\)
Nên \(\left( {{d_3}} \right):y = 3x + b\)
Gọi \(M\left( {{x_M};{y_M}} \right)\) là giao điểm của \(\left( {{d_3}} \right)\) với \(\left( {{d_2}} \right).\)
Theo đề bài ta có : \({x_M} = 2.\)
Vì \(M\) thuộc \(\left( {{d_2}} \right):y = - 2x + 3\) nên \({y_M} = - 2.2 + 3 = - 1.\)
Vì \(M\) thuộc \(\left( {{d_3}} \right):y = 3x + b\) nên \( - 1 = 3.2 + b.\)
Suy ra \(b = - 7\) (nhận).
Vậy \(a = 3;b = - 7.\)
Bài 4 (VD):
Phương pháp:
a) Sử dụng mối quan hệ quãng đường bằng tích vận tốc với thời gian
b) Tìm thời gian xe di chuyển
Từ đó suy ra thời điểm xe xuất phát.
Cách giải:
a) Viết công thức biểu diễn quãng đường \(y\left( {km} \right)\) từ nhà An đến Đà Lạt theo thời gian \(x\) (giờ) mà xe di chuyển từ trường đến Đà Lạt.
Quãng đường An di chuyển từ trường đến Đà Lạt là: \(45x\,\left( {km} \right)\)
Vì nhà An cách trường 3km nên quãng đường An di chuyển từ nhà đến Đà Lạt là: \(y = 3 + 45x\,\,\left( {km} \right)\)
b) Thay \(y = 318\) vào công thức \(y = 45x + 3\) (ở câu a), ta có: \(318 = 45x + 3 \Leftrightarrow 45x = 315 \Leftrightarrow x = 7\)
Hay thời gian xe di chuyển từ trường đến Đà Lạt mất 7h.
Thời điểm xe cần xuất phát từ trường để đến Đà Lạt vào lúc \(15\) giờ là :
\(15 - 7 - 1,5 = 6,5\left( h \right) = 6\) giờ \(30\) phút.
Bài 5 (VD):
Phương pháp:
Tính tiền lãi bác Ba nhận được ở năm đầu tiên
Tính cả gốc và lãi bác Ba nhận được sau năm đầu tiên
Tính tiền lãi bac Ba nhận được ở năm thứ hai
Tính cả gốc và lãi bác Ba nhận được sau hai
Cách giải:
Tiền lãi bác Ba có được ở năm đầu tiên : \(100.7\% \) (triệu đồng)
Tiền vốn và lãi bác Ba có được sau năm đầu tiên :
\(100 + 100.7\% = 100.\left( {1 + 7\% } \right)\) (triệu đồng)
Tiền lãi bác Ba có được ở năm thứ hai : \(100.\left( {1 + 7\% } \right).7\% \) (triệu đồng)
Tiền vốn và lãi bác Ba có được sau hai năm :
\(100.\left( {1 + 7\% } \right) + 100.\left( {1 + 7\% } \right).7\% = 100.{\left( {1 + 7\% } \right)^2}\)\( = 114,49\) (triệu đồng)
Vậy sau hai năm, khi rút tiền ra bác Ba nhận được \(114,49\) triệu đồng = \(114.490.000\) (đồng)
Bài 6 (VD):
Phương pháp:
Sử dụng tính chất tiếp tuyến, hệ thức lượng trong tam giác vuông và các cặp tam giác đồng dạng
Cách giải:
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(A\) nằm ở ngoài đường tròn sao cho \(OA < 2R.\) Vẽ các tiếp tuyến \(AB,\,AC\) ( \(B,C\) là các tiếp điểm). \(BC\) cắt \(OA\) tại \(H\) .
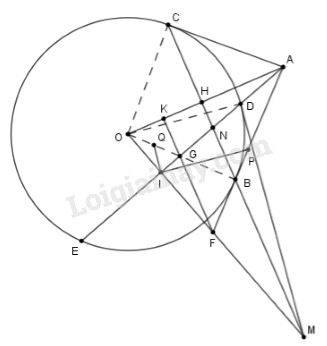
a) Chứng minh \(OA\) vuông góc với \(BC\) và \(OH.OA = {R^2}.\)
Xét \(\left( O \right):\)
\(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\(OB = OC = R\)
Do đó, \(OA\) là trung trực của \(BC.\)
Suy ra \(OA\) vuông góc với \(BC\) tại \(H.\)
Xét \(\Delta BAO\) vuông tại \(B\) (\(AB\) là tiếp tuyến của \(\left( O \right)\) có \(AH\) là đường cao, \(OA\) vuông góc \(BC\) tại \(H\))
\(OH.OA = O{B^2} = {R^2}\) (hệ thức lượng trong tam giác vuông)
b) Vẽ cát tuyến \(ADE\) nằm bên trong góc \(BAO\) ( \(AD\) nhỏ hơn \(AE\) ). Vẽ \(OI\) vuông góc với \(DE\) tại \(I.\) Tia \(OI\) cắt \(AB\) tại \(F.\) Gọi \(G\) là giao điểm của \(DE\) với \(OB\) và \(Q\) là trung điểm của \(OG\) . Tia \(FG\) cắt tia \(AO\) tại \(K.\) Chứng minh \(FK\) vuông góc với \(OA\) và \(QI\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(FIA.\)
Xét tam giác \(AOF\) có \(OB \bot AF,\,AI \bot OF\) và \(OB \cap AI = \left\{ G \right\}\) nên \(G\) là trực tâm của tam giác \(AOF\), nên \(FG\) vuông góc với \(OA\) tại \(K\), tức \(FK\) vuông góc với \(OA.\)
Gọi \(P\) là trung điểm của \(AF.\)
Vì tam giác \(IAF\) vuông tại \(I\) nên \(PA = PF = PI = \dfrac{{AF}}{2}\) hay \(F,\,I,\,A\) thuộc đường tròn đường kính \(AF,\) tâm \(P\) là trung điểm của \(AF.\) Vì \(\Delta IOG\) vuông tại \(I\) có \(Q\) là trung điểm \(OG\) nên \(QI = QO = QG = \dfrac{{OG}}{2}\)
Suy ra \(\Delta QIO\) cân tại \(Q,\) do đó: \(\widehat {QOI} = \widehat {QIO}\)
Ta có \(PI = PF\left( {cmt} \right)\) nên \(\Delta PIF\) cân tại \(P.\) Do đó: \(\widehat {PIF} = \widehat {PFI}\)
Nên \(\widehat {QIO} + \widehat {PIF} = \widehat {IOQ} + \widehat {PFI} = 90^\circ \) (vì \(\Delta FOB\) vuông tại \(B\)).
Suy ra \(\widehat {QIP} = 180^\circ - \left( {\widehat {QIO} + \widehat {PIF}} \right) = 90^\circ \)
Nên \(QI\) vuông góc với \(PI\) tại \(I\) thuộc đường tròn \(\left( {FIA} \right)\).
Vậy \(QI\) là tiếp tuyến của đường tròn \(\left( {FIA} \right).\)
c) Tiếp tuyến tại \(D\) của đường tròn \(\left( {O;R} \right)\) cắt tia \(OF\) tại \(M\) . \(BH\) cắt \(AI\) tại \(N.\) Chứng minh \(\dfrac{2}{{BC}} = \dfrac{1}{{BN}} - \dfrac{1}{{BM}}.\)
Theo câu a) ta có \(OH.OA = {R^2}\)
Xét tam giác \(ODM\) vuông tại \(D\) có \(DI\) là đường cao nên \(OI.OM = O{D^2} = {R^2}\) (hệ thức lượng trong tam giác)
Suy ra \(OH.OA = OI.OM \Rightarrow \dfrac{{OH}}{{OM}} = \dfrac{{OI}}{{OA}}\)
Lại có góc \(AOM\) chung nên \(\Delta OHM\) đồng dạng \(\Delta OIA\) (c-g-c), suy ra \(\widehat {OHM} = \widehat {OIA} = 90^\circ .\)
Suy ra \(HM\) vuông góc với \(OA\) tại \(H.\)
Mà \(BC\) vuông góc \(OA\) tại \(H\).
Nên \(M,B,H\) thẳng hàng.
Xét tam giác \(HMO\) và tam giác \(HAN\) có:
\(\widehat {OHM} = \widehat {AHN} = {90^0},\) \(\widehat {HAN} = \widehat {OMH}\) (cùng phụ với \(\widehat {HOM}\))
Nên \(\Delta HMO\) đồng dạng với \(\Delta HAN\)
Suy ra \(\dfrac{{HM}}{{HO}} = \dfrac{{HA}}{{HN}} \Rightarrow HM.HN = HA.HO\)
Xét tam giác \(OAB\) vuông có \(HA.HO = B{H^2}\) (hệ thức lượng)
Nên \(HN.HM = H{B^2}\,\,\left( { = HO.HA} \right)\)
\( \Leftrightarrow \left( {HB - BN} \right)\left( {HB + BM} \right) = H{B^2}\)
\( \Leftrightarrow H{B^2} + HB.\left( {BM - BN} \right) - BN.BM = H{B^2}\)
\( \Leftrightarrow HB.\left( {BM - BN} \right) = BN.BM\)
\( \Leftrightarrow \dfrac{1}{{HB}} = \dfrac{{BM - BN}}{{BN.BM}}\)
\( \Leftrightarrow \dfrac{1}{{\left( {\dfrac{{BC}}{2}} \right)}} = \dfrac{1}{{BN}} - \dfrac{1}{{BM}}\)
\( \Leftrightarrow \dfrac{2}{{BC}} = \dfrac{1}{{BN}} - \dfrac{1}{{BM}}\)
Bài 7 (VD):
Phương pháp:
Sử dụng tỉ số lượng giác của góc nhọn
Cách giải:
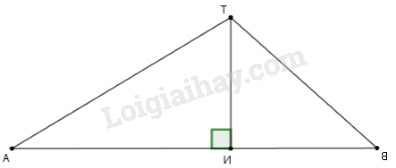
\(\Delta TAN\left( {\widehat N = 90^\circ } \right):\tan A = \dfrac{{TN}}{{AN}}\)
Nên: \(TN = AN.\tan A = BN.\tan B\)
\(\begin{array}{l} \Leftrightarrow \left( {NB + AB} \right).\tan A = BN.\tan B\\ \Leftrightarrow \left( {\tan B - \tan A} \right).NB = AB.\tan A\\ \Leftrightarrow NB = \dfrac{{AB.\tan A}}{{\tan B - \tan A}}\end{array}\)
Suy ra
\(\begin{array}{l}TN = NB.\tan B = \dfrac{{AB.\tan A.\tan B}}{{\tan B - \tan A}}\\TN = \dfrac{{1500.\tan 41,2^\circ .\tan 29,7^\circ }}{{\tan 41,2^\circ - \tan 29,7^\circ }} \approx 2455,4\end{array}\)
Vậy chiều cao ngọn núi \(TN\) khoảng \(2455,4\) mét.
HẾT