Giải đề thi học kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Ba Đình — Không quảng cáo

Bài 1  (2,0 điểm):

a) Rút gọn biểu thức: $A = \dfrac{2}{{\sqrt 3  - 2}} + \dfrac{{\sqrt {12} }}{2} + \sqrt 3$.

b) Một chiếc thang dài $3,5m$. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn là $75^\circ$ (làm tròn kết quả đến chữ số thập phân thứ nhất).

Bài 2 (2,0 điểm): Cho hai biểu thức

$A = \dfrac{{x + 5\sqrt x }}{{x - 25}}\,\,;\\B = \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{x + 9\sqrt x }}{{x - 9}}$  với $x \ge 0$ và $x \ne 9$ và $x \ne 25$.

a) Tìm $x$ để biểu thức $A$ nhận giá trị bằng $0$.

b) Rút gọn biểu thức $B$.

c) Đặt $P = B:A$. So sánh $P$ với $1$.

Bài 3 (2,0 điểm):

Trên mặt phẳng tọa độ $Oxy$, cho đường thẳng $\left( d \right):\,\,y = \left( {m - 1} \right)x - m$ (với $m$là tham số).

a) Vẽ đường thẳng $\left( d \right)$ khi $m = 3$;

b) Tìm $m$ để $\left( d \right)$ đi qua điểm $A\left( { - 1; - 3} \right)$;

c) Tìm $m$ để $\left( d \right)$ cùng với hai đường thẳng $\left( {{d_1}} \right):\,\,y = x - \dfrac{2}{3}$ và $\left( {{d_2}} \right):\,\,y =  - x + 1$ đồng quy.

Bài 4 (3,5 điểm): Cho điểm $C$ thuộc đường tròn tâm $O$ đường kính $AB,\,\,\left( {AC < BC} \right)$. Gọi $H$ là trung điểm $BC$. Tiếp tuyến tại $B$ của đường tròn $\left( O \right)$ cắt tia $OH$ tại $D$.

a) Chứng minh rằng: $DH.DO = D{B^2}$;

b) Chứng minh $DC$ là tiếp tuyến của đường tròn $\left( O \right)$;

c) Đường thẳng $AD$ cắt đường tròn $\left( O \right)$ tại $E$. Gọi $M$ là trung điểm $AE$. Chứng minh bốn điểm $D,B,M,C$ cùng thuộc một đường tròn.

d) Gọi $I$ là trung điểm $DH,BI$ cắt đường tròn $\left( O \right)$ tại $F.$ Chứng minh ba điểm $A,H,F$ thẳng hàng.

Bài 5 (3 điểm): Giải phương trình: $\sqrt 2 \left( {{x^2} + 8} \right) = 5\sqrt {{x^3} + 8}$.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Bài 1 (VD):

Phương pháp:

a)  Khử mẫu biểu thức lấy căn $\dfrac{1}{{\sqrt A  - B}} = \dfrac{{\sqrt A  + B}}{{A - {B^2}}}\,\left( {A \ge 0;\,A \ne {B^2}} \right)$ và sử dụng $\sqrt {{A^2}B}  = \left| A \right|B\,\left( {B \ge 0} \right)$

b) Sử dụng quan hệ giữa cạnh và góc trong tam giác vuông

Cách giải:

a) Rút gọn biểu thức: $A = \dfrac{2}{{\sqrt 3  - 2}} + \dfrac{{\sqrt {12} }}{2} + \sqrt 3$ .

$A = \dfrac{2}{{\sqrt 3  - 2}} + \dfrac{{\sqrt {12} }}{2} + \sqrt 3$$= \dfrac{{2\left( {\sqrt 3  + 2} \right)}}{{3 - 4}} + \dfrac{{\sqrt {4.3} }}{2} + \sqrt 3$ $=  - 2\sqrt 3  - 4 + \sqrt 3  + \sqrt 3  =  - 4$

b) Một chiếc thang dài $3,5m$ . Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn là $75^\circ$ (làm tròn kết quả đến chữ số thập phân thứ nhất).

Xét hình vẽ:

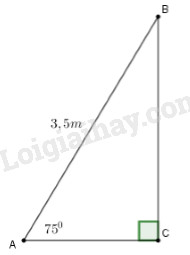
Do:

- Tường nhà tạo với phương ngang của mặt đất góc $90^\circ$;

- Góc an toàn mà thang tạo với mặt đất là $75^\circ$.

Nên: ta xét $\Delta ABC$ vuông tại $C$; độ dài cạnh $AB$ bằng chiều dài của thang tức $AB = 3,5m$; cạnh $AC$ là khoảng cách cần tính.

Xét $\Delta ABC$ vuông tại $C$:

$\begin{array}{l}AC = AB.\cos A\,\,\,\left( {dl} \right)\\ = 3,5.\cos 75^\circ  \approx 0,9\,\,\left( m \right)\end{array}$

Bài 2 (VD):

Phương pháp:

a) Đưa về dạng $A\left( x \right)B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.$

b) Qui đồng mẫu, cộng trừ các phân thức rồi rút gọn

c) Tính $P.$ Xét hiệu $P - 1$ rồi so sánh hiệu đó với $0.$

Cách giải:

Cho hai biểu thức

$A = \dfrac{{x + 5\sqrt x }}{{x - 25}}\,\,;\,\,\,\,\,\,B = \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{x + 9\sqrt x }}{{x - 9}}$ ,  với $x \ge 0$ và $x \ne 9$ và $x \ne 25$ .

a) Tìm $x$ để biểu thức $A$ nhận giá trị bằng $0$ .

$\begin{array}{l}A = 0 \Leftrightarrow x + 5\sqrt x  = 0\\ \Leftrightarrow \sqrt x \left( {\sqrt x  + 5} \right) = 0,\,\,\,do\,\,\sqrt x  + 5 > 0\\ \Leftrightarrow \sqrt x  = 0 \Leftrightarrow x = 0\,\,\left( {tm} \right)\end{array}$

b) Rút gọn biểu thức $B$ .

$\begin{array}{l}B = \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{x + 9\sqrt x }}{{x - 9}}\\ = \dfrac{{2\sqrt x \left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} - \dfrac{{x + 9\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{2x + 6\sqrt x  - x - 9\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} \\= \dfrac{{x - 3\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{\sqrt x }}{{\sqrt x  + 3}}\end{array}$

c) Đặt $P = B:A$ . So sánh $P$ với $1$ .

$\begin{array}{l}\,P = B:A = \dfrac{{\sqrt x }}{{\sqrt x  + 3}}:\dfrac{{x + 5\sqrt x }}{{x - 25}}\\P = \dfrac{{\sqrt x }}{{\sqrt x  + 3}}:\dfrac{{\sqrt x }}{{\sqrt x  - 5}} \\= \dfrac{{\sqrt x }}{{\sqrt x  + 3}}.\dfrac{{\sqrt x  - 5}}{{\sqrt x }}\\P = \dfrac{{\sqrt x  - 5}}{{\sqrt x  + 3}}\end{array}$

Xét hiệu

$P - 1 = \dfrac{{\sqrt x  - 5}}{{\sqrt x  + 3}} - 1 = \dfrac{{ - 8}}{{\sqrt x  + 3}}$

Vì $- 8 < 0$ và $\sqrt x  + 3 > 0$ với mọi $x \ge 0;x \ne \left\{ {9;25} \right\}$ nên $P - 1 = \dfrac{{ - 8}}{{\sqrt x  + 3}} < 0 \Leftrightarrow P < 1$

Bài 3 (VD):

Phương pháp:

a) Tìm tọa độ 2 điểm thuộc đồ thị rồi vẽ đường thẳng qua hai điểm đó

b) Thay tọa độ điểm A vào hàm số để tìm m

c) Tìm giao điểm của $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right).$ Thay tọa độ giao điểm tìm được vào phương trình đường thẳng $\left( d \right).$

Cách giải:

Trên mặt phẳng tọa độ $Oxy$ , cho đường thẳng $\left( d \right):\,\,y = \left( {m - 1} \right)x - m$ (với $m$ là tham số).

a) Vẽ đường thẳng $\left( d \right)$ khi $m = 3$

Khi $m = 3$, phương trình đường thẳng $\left( d \right):\,\,y = 2x - 3$

$\begin{array}{l}x = 0 \Rightarrow y =  - 3 \Rightarrow \left( {0; - 3} \right) \in \left( d \right)\\y = 0 \Rightarrow x = \dfrac{3}{2} \Rightarrow \left( {\dfrac{3}{2};0} \right) \in \left( d \right)\end{array}$

Đồ thị :

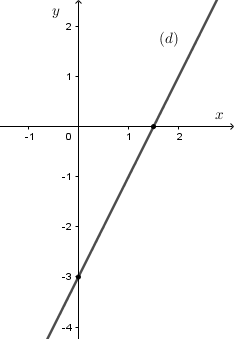
b) Tìm $m$ để $\left( d \right)$ đi qua điểm $A\left( { - 1; - 3} \right)$

Đường thẳng $\left( d \right)$ đi qua điểm $A\left( { - 1; - 3} \right)$

$\Leftrightarrow x =  - 1;y =  - 3$ thỏa mãn phương trình của $\left( d \right)$

$\begin{array}{l} \Leftrightarrow  - 3 = \left( {m - 1} \right).\left( { - 1} \right) - m\\ \Leftrightarrow m = 2\end{array}$

Vậy với $m = 2$ thì đường thẳng $\left( d \right)$ đi qua điểm $A\left( { - 1; - 3} \right)$.

c) Tìm $m$ để $\left( d \right)$ cùng với hai đường thẳng $\left( {{d_1}} \right):\,\,y = x - \dfrac{2}{3}$ và $\left( {{d_2}} \right):\,\,y =  - x + 1$ đồng quy.

Xét phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$:

$x - \dfrac{2}{3} =  - x + 1 \Leftrightarrow x = \dfrac{5}{6}$ $\Rightarrow y = \dfrac{1}{6}$

$\Rightarrow M\left( {\dfrac{5}{6};\dfrac{1}{6}} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.

Để ${d_1},\,\,{d_2},\,\,{d_3}$ đồng quy $\Leftrightarrow M\left( {\dfrac{5}{6};\dfrac{1}{6}} \right) \in d$

$\Leftrightarrow x = \dfrac{5}{6};y = \dfrac{1}{6}$ thỏa mãn phương trình của $\left( d \right)$

$\begin{array}{l} \Leftrightarrow \dfrac{1}{6} = \left( {m - 1} \right).\dfrac{5}{6} - m\\ \Leftrightarrow m =  - 6\end{array}$

Vậy với $m = 2$ thì ba đường thẳng ${d_1},\,\,{d_2},\,\,{d_3}$ đồng quy.

Bài 4 (VD):

Phương pháp:

a) Sử dụng hệ thức lượng trong tam giác vuông

b) Sử dụng tính chất hai tam giác bằng nhau để có $OC \bot CD.$

c) Sử dụng: Đường tròn ngoại tiếp tam giác vuông nhận cạnh huyền làm đường kính

d) Sử dụng tính chất đường trung bình của tam giác và quan hệ từ vuông góc đến song song

Cách giải:

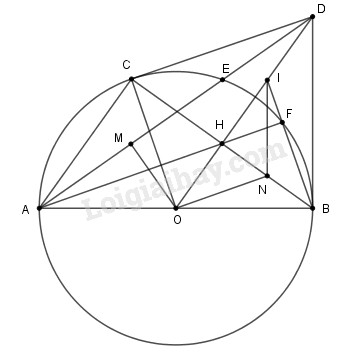
a) Chứng minh rằng: $DH.DO = D{B^2}$

Vì $BD$ là tiếp tuyến của đường tròn $\left( O \right)$ nên $\Delta OBD$ vuông tại $B$;

Xét đường tròn $\left( O \right)$ có $OH$ là 1 phân đường kính và $BC$ là dây cung có $H$ là trung điểm nên $BH \bot OD$

Xét $\Delta OBD$: $\widehat {OBD} = 90^\circ ;\,\,BH \bot OD$$\Rightarrow DH.DO = B{D^2}$ (hệ thức lượng trong tam giác vuông)

b) Chứng minh $DC$ là tiếp tuyến của đường tròn $\left( O \right)$

Ta có $\Delta COB$ cân tại $O$ (vì $OC = OB$) có $OH$ là trung tuyến $\Rightarrow OH$ là phân giác (t/c)

$\Rightarrow \widehat {COD} = \widehat {BOD}$

Xét tam giác $COD$ và tam giác $BOD$ có:

+) $OC = OB$ (= bán kính)

+) $\widehat {COD} = \widehat {BOD}\,\left( {cmt} \right)$

+) Cạnh $OD$ chung

Nên $\Delta COD = \Delta BOD\,\left( {c.g.c} \right)$$\Rightarrow \widehat {OCD} = \widehat {OBD} = 90^\circ$$\Rightarrow OC \bot CD$

Suy ra $CD$ là tiếp tuyến của $\left( O \right)$.

c) Đường thẳng $AD$ cắt đường tròn $\left( O \right)$ tại $E$ . Gọi $M$ là trung điểm $AE$ . Chứng minh bốn điểm $D,B,M,C$ cùng thuộc một đường tròn.

Xét đường tròn $\left( O \right)$ có $M$ là trung điểm $AE$, $OM$ là đường kính, $AE$ là dây không đi qua $O$

$OM \bot AE\,\,\left( {dl} \right)$

Từ đó ta có $\widehat {OCD} = \widehat {OBD} = \widehat {OMD} = 90^\circ$

$\Rightarrow D,B,M,C$ cùng thuộc đường tròn đường kính $OD$

d) Gọi $I$ là trung điểm $DH,BI$ cắt đường tròn $\left( O \right)$ tại $F.$ Chứng minh ba điểm $A,H,F$ thẳng hàng.

Lấy $N$ là trung điểm của $HB$$\Rightarrow IN$ là đường trung bình của $\Delta DHB$

Suy ra $NI//DB$ mà $DB \bot AB \Rightarrow IN \bot AB$

Xét tam giác $IOB$ có hai đường cao $IN$ và $BH$ giao nhau tại $N$$\Rightarrow N$ là trực tâm $\Delta IOB$

$\Rightarrow ON \bot BI$

Lại có $ON$ là đường trung bình của $\Delta AHB$ nên $ON//AH$

Mà $ON \bot BI$ $\Rightarrow AH \bot BI$  (1)

Xét $\left( O \right)$ có $AB$ là đường kính và $F \in \left( O \right)$ nên $AF \bot BF$ hay $AF \bot BI$ (2)

Từ (1) và (2) $\Rightarrow A,H,F$ thẳng hàng.

Bài 5 (VDC):

Phương pháp:

Bình phương hai vế rồi phân tích vế trái thành nhân tử đưa về dạng $A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.$

Cách giải:

ĐK : $x \ge  - 2$.

Bình phương 2 vế không âm ta được:

$\begin{array}{l}\sqrt 2 \left( {{x^2} + 8} \right) = 5\sqrt {{x^3} + 8} \\ \Leftrightarrow 2{\left( {{x^2} + 8} \right)^2} = 25.\left( {{x^3} + 8} \right)\\ \Leftrightarrow 2{x^4} - 25{x^3} + 32{x^2} - 72 = 0\end{array}$

$\Leftrightarrow 2{x^4} - 20{x^3} - 24{x^2} - 5{x^3} + 50{x^2}$$+ 60x + 6{x^2} - 60x - 72 = 0$

$\Leftrightarrow 2{x^2}\left( {{x^2} - 10x - 12} \right) - 5x\left( {{x^2} - 10x - 12} \right)$$+ 6\left( {{x^2} - 10x - 12} \right) = 0$

$\Leftrightarrow \left( {2{x^2} - 5x + 6} \right)\left( {{x^2} - 10x - 12} \right) = 0$

Do $2{x^2} - 5x + 6 = 2{\left( {x - \dfrac{5}{4}} \right)^2} + \dfrac{{23}}{8} > 0$

Nên ${x^2} - 10x - 12 = 0$$\Leftrightarrow {\left( {x - 5} \right)^2} = 37 \Leftrightarrow \left[ \begin{array}{l}x - 5 = \sqrt {37} \\x - 5 =  - \sqrt {37} \end{array} \right.$

$\Rightarrow {x_2} = 5 + \sqrt {37} \,\,;\,\,\,\,\,{x_2} = 5 - \sqrt {37}$  (thỏa mãn)

Vậy $x = 5 \pm \sqrt {37} .$

HẾT