Giải đề thi học kì 1 toán lớp 9 năm 2019 - 2020 PGD huyện Thanh Trì — Không quảng cáo

Bài 1 (2,0 điểm): Rút gọn các biểu thức

$\begin{array}{l}A = 3\sqrt {\dfrac{1}{3}}  + \dfrac{1}{2}\sqrt {48}  + \sqrt {75} \\B = 3\sqrt {20}  - 20\sqrt {\dfrac{1}{5}}  - \dfrac{4}{{\sqrt 5  + \sqrt 3 }}\end{array}$

Bài 2 (2,0 điểm): Cho hai biểu thức $A = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}$ và $B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} + \dfrac{{6\sqrt x  - 4}}{{1 - x}}$ $\left( {x \ge 0;\,\,x \ne 1} \right)$.

a) Tính giá trị của biểu thức $A$ khi $x = 9$.

b) Rút gọn $B$.

c) Đặt $P = A.B$. So sánh giá trị của $P$ với $2$.

Bài 3 (1,5 điểm): Cho hàm số $y = \left( {m - 1} \right)x - 4$ có đồ thị là đường thẳng $\left( d \right)$.

a) Tìm $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 5$.

b) Vẽ đồ thị hàm số trên với $m$ tìm được ở câu a.

c) Đường thẳng $\left( d \right)$ cắt trục $Ox$ tại $A$,  cắt trục $Oy$ tại $B$. Tìm $m$ để tam giác $OAB$ vuông cân.

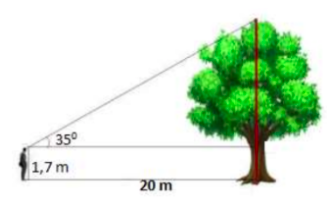
Bài 4 (1,0 điểm): Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)

Bài 5 (3,0 điểm): Cho đường tròn $\left( O \right)$ và một điểm $M$ nằm ngoài đường tròn. Từ $M$ kẻ hai tiếp tuyến $MA,MB$ với đường tròn $\left( O \right)$ ($A$ và $B$là hai tiếp điểm). Gọi $I$ là giao điểm của $OM$ và $AB$. Kẻ đường kính $BC$ của $\left( O \right)$.

a) Chứng minh $4$ điểm $M,O,A,B$ cùng thuộc một đường tròn.

b) Chứng minh $OI.OM = O{A^2}$.

c) Qua $\left( O \right)$ vẽ đường thẳng vuông góc với $MC$ tại $E$ và cắt đường thẳng $BA$ tại $F$. Chứng minh $FC$ là tiếp tuyến của đường tròn $\left( O \right)$.

Bài 6 (0,5 điểm): Cho ba số dương $x,y,z$ thay đổi nhưng luôn thỏa mãn điều kiện $x + y + z = 1$. Tìm giá trị lớn nhất của biểu thức: $P = \dfrac{x}{{x + 1}} + \dfrac{y}{{y + 1}} + \dfrac{z}{{z + 1}}$.

HƯỚNG DẪN GIẢI CHI TIẾT

Bài 1(VD): Rút gọn các biểu thức

$\begin{array}{l}A = 3\sqrt {\dfrac{1}{3}}  + \dfrac{1}{2}\sqrt {48}  + \sqrt {75} \\B = 3\sqrt {20}  - 20\sqrt {\dfrac{1}{5}}  - \dfrac{4}{{\sqrt 5  + \sqrt 3 }}\end{array}$

Phương pháp

Đưa thừa số ra ngoài dấu căn $\sqrt {{A^2}B}  = \left| A \right|\sqrt B$.

Trục căn thức ở mẫu $\dfrac{C}{{\sqrt A  + \sqrt B }} = \dfrac{{C\left( {\sqrt A  - \sqrt B } \right)}}{{A - B}}$.

Cách giải:

+) Ta có :

$A = 3\sqrt {\dfrac{1}{3}}  + \dfrac{1}{2}\sqrt {48}  + \sqrt {75}$$= 3.\dfrac{{\sqrt 3 }}{3} + \dfrac{1}{2}.4\sqrt 3  + 5\sqrt 3$ $= \sqrt 3  + 2\sqrt 3  + 5\sqrt 3  = 8\sqrt 3$

+) Ta có:

$B = 3\sqrt {20}  - 20\sqrt {\dfrac{1}{5}}  - \dfrac{4}{{\sqrt 5  + \sqrt 3 }}$$= 3.2\sqrt 5  - 20.\dfrac{{\sqrt 5 }}{5} - \dfrac{{4\left( {\sqrt 5  - \sqrt 3 } \right)}}{{\left( {\sqrt 5  + \sqrt 3 } \right)\left( {\sqrt 5  - \sqrt 3 } \right)}}$

$B = 6\sqrt 5  - 4\sqrt 5  - \dfrac{{4\left( {\sqrt 5  - \sqrt 3 } \right)}}{{5 - 3}}$$= 2\sqrt 5  - 2\sqrt 5  + 2\sqrt 3  = 2\sqrt 3$.

Bài 2 (VD) : Cho hai biểu thức $A = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}$ và $B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} + \dfrac{{6\sqrt x  - 4}}{{1 - x}}$ $\left( {x \ge 0;\,\,x \ne 1} \right)$.

a) Tính giá trị của biểu thức $A$ khi $x = 9$.

b) Rút gọn $B$.

c) Đặt $P = A.B$. So sánh giá trị của $P$ với $2$.

Phương pháp

a) Thay $x = 9$ vào $A$ và tính giá trị.

b) Qui đồng, khử mẫu và rút gọn.

c) Tính $P = AB$ và xét dấu của hiệu $P - 2$.

Cách giải:

a) Tính giá trị của biểu thức $A$ khi $x = 9$ .

Thay $x = 9$ (TMĐK) vào biểu thức $A$, ta có : $A = \dfrac{{2\sqrt 9  - 4}}{{\sqrt 9  - 1}} = \dfrac{{2.3 - 4}}{{3 - 1}} = \dfrac{2}{2} = 1$

Vậy với $x = 9$ thì $A = 1.$

b) Rút gọn $B$ .

$B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} + \dfrac{{6\sqrt x  - 4}}{{1 - x}}$ $\left( {x \ge 0;\,\,x \ne 1} \right)$.

$B = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} - \dfrac{{6\sqrt x  - 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}$$= \dfrac{{\sqrt x \left( {\sqrt x  + 1} \right) + 3\left( {\sqrt x  - 1} \right) - 6\sqrt x  + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}$

$B = \dfrac{{x + \sqrt x  + 3\sqrt x  - 3 - 6\sqrt x  + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}$$= \dfrac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} = \dfrac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}$$= \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}$

Vậy $B = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}$ với $x \ge 0;\,\,x \ne 1$.

c) Đặt $P = A.B$ . So sánh giá trị của $P$ với $2$ .

Có $P = A.B = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}.\dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}} = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  + 1}}$

Xét $P - 2 = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  + 1}} - 2$$= \dfrac{{2\sqrt x  - 4 - 2\sqrt x  - 2}}{{\sqrt x  + 1}} = \dfrac{{ - 6}}{{\sqrt x  + 1}}$

Vì $- 6 < 0;\,\,\sqrt x  + 1 \ge 0$ với mọi $x \ge 0;\,\,x \ne 1$

$\Rightarrow \dfrac{{ - 6}}{{\sqrt x  + 1}} < 0$ $\Rightarrow P - 2 < 0 \Rightarrow P < 2$.

Vậy $P < 2$.

Bài 3 (VD) : Cho hàm số $y = \left( {m - 1} \right)x - 4$ có đồ thị là đường thẳng $\left( d \right)$.

a) Tìm $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 5$.

b) Vẽ đồ thị hàm số trên với $m$ tìm được ở câu a.

c) Đường thẳng $\left( d \right)$ cắt trục $Ox$ tại $A$,  cắt trục $Oy$ tại $B$. Tìm $m$ để tam giác $OAB$ vuông cân.

Phương pháp

a) Đường thẳng $d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$.

b) Cho lần lượt $x = 0,y = 0$ tìm tọa độ các điểm đi qua và vẽ đồ thị.

c) Tìm tọa độ $A,B$.

Để $\Delta OAB$ vuông cân tại$O$$\Rightarrow OA = OB$

Cách giải:

a) Tìm $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 5$ .

Đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 5$ khi $\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\ - 4 \ne 5\end{array} \right. \Leftrightarrow m = 3$.

Vậy $m = 3$ thì thỏa mãn bài toán.

b) Vẽ đồ thị hàm số trên với $m$ tìm được ở câu a.

Với $m = 3$, ta có : $\left( d \right):\,\,y = 2x - 4$.

Cho $x = 0$ ta được $y = 2.0 - 4 =  - 4$ nên $M\left( {0; - 4} \right)$.

Cho $y = 0 \Rightarrow 0 = 2x - 4 \Leftrightarrow x = 2$ nên $N\left( {2;0} \right)$.

Đồ thị hàm số là đường thẳng $\left( d \right)$ đi qua hai điểm $\left( {0; - 4} \right)$ và $\left( {2;0} \right)$

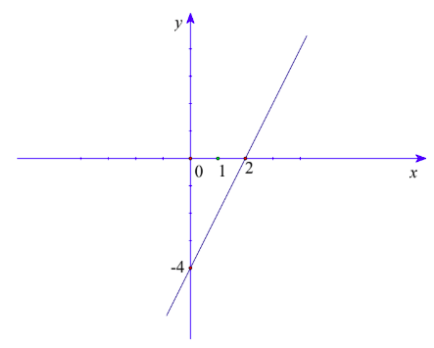
c) Đường thẳng $\left( d \right)$ cắt trục $Ox$ tại $A$ ,  cắt trục $Oy$ tại $B$ . Tìm $m$ để tam giác $OAB$ vuông cân.

$\left( d \right)$ cắt hai trục $Ox;Oy$ tại $A,\,\,B$ thì $m - 1 \ne 0 \Leftrightarrow m \ne 1$.

Cho $x = 0 \Rightarrow y =  - 4$$\Rightarrow B\left( {0; - 4} \right) \Rightarrow OB = \left| { - 4} \right| = 4$.

Cho $y = 0 \Rightarrow x = \dfrac{4}{{m - 1}}$$\Rightarrow A\left( {\dfrac{4}{{m - 1}};0} \right) \Rightarrow OA = \dfrac{4}{{\left| {m - 1} \right|}}$

Để $\Delta OAB$ vuông cân tại$O$$\Rightarrow OA = OB$

$\Leftrightarrow \dfrac{4}{{\left| {m - 1} \right|}} = 4 \Leftrightarrow \left| {m - 1} \right| = 1 \\\Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.(TM )$

Vậy $m \in \left\{ {0;2} \right\}$.

Bài 4 (TH) : Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)

Phương pháp

Sử dụng giá trị lượng giác của một góc nhọn trong tam giác vuông để giải tam giác.

Cách giải:

Chiều cao của cây là : $h = 1,7 + 20.\tan 35^\circ  \approx 15,7m$.

Bài 5 (VD) : Cho đường tròn $\left( O \right)$ và một điểm $M$ nằm ngoài đường tròn. Từ $M$ kẻ hai tiếp tuyến $MA,MB$ với đường tròn $\left( O \right)$ ( $A$ và $B$ là hai tiếp điểm). Gọi $I$ là giao điểm của $OM$ và $AB$ . Kẻ đường kính $BC$ của $\left( O \right)$ .

a) Chứng minh $4$ điểm $M,O,A,B$ cùng thuộc một đường tròn.

b) Chứng minh $OI.OM = O{A^2}$.

c) Qua $\left( O \right)$ vẽ đường thẳng vuông góc với $MC$ tại $E$ và cắt đường thẳng $BA$ tại $F$. Chứng minh $FC$ là tiếp tuyến của đường tròn $\left( O \right)$.

Phương pháp

a) Gọi $K$ là trung điểm $OM$, chứng minh $KO = KM = KA = KB$ dựa vào tính chất tam giác vuông.

b) Sử dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $OAM$.

c) Chứng minh $\Delta OCE \sim \Delta OFC\left( {c.g.c} \right)$ suy ra $\widehat {OCF} = \widehat {OEC} = 90^\circ$.

Cách giải:

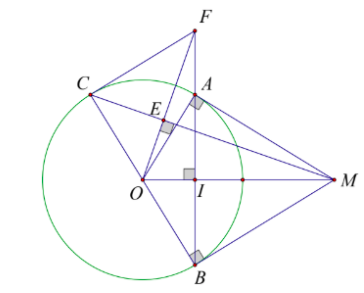
a) Chứng minh $4$ điểm $M,O,A,B$ cùng thuộc một đường tròn.

Gọi $K$ là trung điểm của $OM$$\Rightarrow OK = KM$.

Tam giác $OAM$ vuông tại $A$ nên $AK = KM = KO = \dfrac{1}{2}OM$(tính chất trung tuyến tam giác vuông).

Tam giác $OBM$ vuông tại $B$ nên $BK = KM = KO = \dfrac{1}{2}OM$(tính chất trung tuyến tam giác vuông).

Do đó $OK = KM = KA = KB$.

Suy ra $4$ điểm $O,A,M,B$ nằm trên đường tròn tâm $K$, đường kính $OM$.

b) Chứng minh $OI.OM = O{A^2}$ .

Ta có : $OA = OB$ (bán kính)

$MA = MB$ (tính chất hai tiếp tuyến cắt nhau)

$\Rightarrow OM$ là trung trực của $AB$$\Rightarrow OM \bot AB$ tại $I$.

$\Delta OAM$ vuông tại $A$ đường cao $AI$ $\Rightarrow OI.OM = O{A^2}$ (hệ thức giữa cạnh và đường cao).

c) Qua $\left( O \right)$ vẽ đường thẳng vuông góc với $MC$ tại $E$ và cắt đường thẳng $BA$ tại $F$ .

Xét $\Delta OFI$ và $\Delta OME$ có :

$\widehat O$ chung

$\widehat {OIF} = \widehat {OEM} = {90^0}$

$\Rightarrow \Delta OFI \sim \Delta OME\left( {g - g} \right)$ nên $\dfrac{{OF}}{{OM}} = \dfrac{{OI}}{{OE}}$(cạnh t/ư)

$\Rightarrow OF.OE = OI.OM = O{A^2} = O{C^2}$

$\Rightarrow \dfrac{{OF}}{{OC}} = \dfrac{{OC}}{{OE}}$

Xét $\Delta OCE$ và $\Delta OFC$ có :

Chung $\widehat O$

$\dfrac{{OF}}{{OC}} = \dfrac{{OC}}{{OE}}\left( {cmt} \right)$

$\Rightarrow \Delta OCE \sim \Delta OFC\left( {c.g.c} \right)$

Nên $\widehat {OCF} = \widehat {OEC} = 90^\circ$(góc t/ư)$\Rightarrow FC$ là tiếp tuyến của $\left( O \right)$ (đpcm).

Bài 6(VDC) : Cho ba số dương $x,y,z$ thay đổi nhưng luôn thỏa mãn điều kiện $x + y + z = 1$ . Tìm giá trị lớn nhất của biểu thức: $P = \dfrac{x}{{x + 1}} + \dfrac{y}{{y + 1}} + \dfrac{z}{{z + 1}}$ .

Phương pháp

Nhận xét : $P = 3 - \left( {\dfrac{1}{{x + 1}} + \dfrac{1}{{y + 1}} + \dfrac{1}{{z + 1}}} \right)$

Sử dụng bất đẳng thức $\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{9}{{a + b + c}}$ để đánh giá.

Cách giải:

Ta có : $P = 3 - \left( {\dfrac{1}{{x + 1}} + \dfrac{1}{{y + 1}} + \dfrac{1}{{z + 1}}} \right)$

Mà $\dfrac{1}{{x + 1}} + \dfrac{1}{{y + 1}} + \dfrac{1}{{z + 1}} \ge \dfrac{9}{{x + y + z + 3}} = \dfrac{9}{4}$

$\Rightarrow P \le 3 - \dfrac{9}{4} = \dfrac{3}{4}$

Dấu  xảy ra khi $x = y = z = \dfrac{1}{3}$.

Vạy $\max P = \dfrac{3}{4} \Leftrightarrow x = y = z = \dfrac{1}{3}$.