Giải đề thi học kì 1 toán lớp 9 năm 2019 - 2020 PGD Thanh Xuân — Không quảng cáo

Bài 1  (2,0 điểm):

1. Rút gọn biểu thức : $A = \dfrac{{\sin 15^\circ  + \cos 15^\circ }}{{\cos 15^\circ }} - \cot 75^\circ .$

2. Giải phương trình : $\sqrt {25x + 5}  + \sqrt {45} \sqrt {20x + 4}  - \sqrt {\dfrac{{5x + 1}}{{16}}}  = \dfrac{{27\sqrt 5 }}{4}.$

Bài 2 (2,0 điểm):

Cho hai biểu thức  $P = \dfrac{2}{{\sqrt 2  - \sqrt x }} - \dfrac{{\sqrt x  + \sqrt 2 }}{{\sqrt {2x}  - x}}$ và $Q = \dfrac{1}{{\sqrt x  - \sqrt {x - 1} }} - \dfrac{{x - 3}}{{\sqrt {x - 1}  - \sqrt 2 }};$ với $x > 1$ và $x \ne 2,\,x \ne 3.$

1) Tính giá trị của biểu thức $P$ khi $x = 16.$

2) Chứng minh rằng $Q + \sqrt 2  = \sqrt x .$

3) Tìm $x$ để $P.Q \ge 0.$

Bài 3 (2,0 điểm):

Cho hai hàm số bậc nhất $y = \left( {m + 1} \right)x + 2m$ và $y = \left( {2m + 1} \right)x + 3m$

1) Tìm giá trị của $m$ để đồ thị của hai hàm số đã cho là hai đường thẳng song song.

2) Tìm giá trị của $m$ để giao điểm của hai đồ thị đã cho nằm trên trục hoành.

Bài 4 (3,5 điểm):

Cho nửa đường tròn $\left( {O;R} \right)$ đường kính $AB.$ Gọi $C,D$ là hai điểm di chuyển trên cung tròn sao cho góc $COD$ luôn bằng $90^\circ$ ($C$ nằm giữa $A$ và $D$). Tiếp tuyến tại $C,D$ cắt đường thẳng $AB$ lần lượt tại $F,G.$ Gọi $E$ là giao điểm của $FC$ và $GD.$

1) Tính chu vi của tam giác $ECD$ theo $R.$

2) Khi tứ giác $FCDG$ là hình thang cân. Hãy tính tỉ số $\dfrac{{AB}}{{FG}}.$

3) Chứng minh rằng $FC.DG$ luôn là hằng số.

4) Tìm vị trí của $C,D$ sao cho tích $AD.BC$ đạt giá trị lớn nhất.

Bài 5 (0,5 điểm):

Với hai số dương $x,y$ thỏa mãn $x + y = 2.$ Tìm giá trị lớn nhất của biểu thức

$T = \sqrt {1 + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{{\left( {x + 1} \right)}^2}}}}  + \sqrt {1 + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{{\left( {y + 1} \right)}^2}}}}  + \dfrac{4}{{\left( {x + 1} \right)\left( {y + 1} \right)}}$

HƯỚNG DẪN GIẢI CHI TIẾT

Bài 1 (VD):

Phương pháp:

1)  Sử dụng $\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}$  và $\cot \alpha  = \tan \beta$ với $\alpha  + \beta  = {90^0}.$

2) Sử dụng công thức $\sqrt {{A^2}B}  = \left| A \right|.B\,\,\left( {B \ge 0} \right)$

Biến đổi đưa phương trình về dạng $\sqrt A  = m\left( {m \ge 0} \right) \Leftrightarrow A = {m^2}\,\left( {A \ge 0} \right)$

Cách giải:

1) Rút gọn biểu thức : $A = \dfrac{{\sin 15^\circ  + \cos 15^\circ }}{{\cos 15^\circ }} - \cot 75^\circ .$

$A = \dfrac{{\sin 15^\circ  + \cos 15^\circ }}{{\cos 15^\circ }} - \cot 75^\circ  \\= \tan 15^\circ  + 1 - \cot 75^\circ$

$= \tan 15^\circ  + 1 - \cot 75^\circ  \\= \tan 15^\circ  + 1 - \tan 15^\circ  = 1$

2) Giải phương trình : $\sqrt {25x + 5}  + \sqrt {45} \sqrt {20x + 4}  - \sqrt {\dfrac{{5x + 1}}{{16}}}  = \dfrac{{27\sqrt 5 }}{4}.$

Điều kiện: $x \ge  - \dfrac{1}{5}$

$\sqrt {25x + 5}  + \sqrt {45} \sqrt {20x + 4}  - \sqrt {\dfrac{{5x + 1}}{{16}}}  = \dfrac{{27\sqrt 5 }}{4}$

$\Leftrightarrow \sqrt 5 .\sqrt {5x + 1}  + 6\sqrt 5 .\sqrt {5x + 1}  - \dfrac{{\sqrt {5x + 1} }}{4} = \dfrac{{27\sqrt 5 }}{4}$ ĐK : $x \ge \dfrac{{ - 1}}{5}$

$\Leftrightarrow \left( {7\sqrt 5  - \dfrac{1}{4}} \right)\sqrt {5x + 1}  = \dfrac{{27\sqrt 5 }}{4}$

$\Leftrightarrow \sqrt {5x + 1}  = \dfrac{{27\sqrt 5 }}{{28\sqrt 5  - 1}}$

$\Leftrightarrow 5x + 1 = {\left( {\dfrac{{27\sqrt 5 }}{{28\sqrt 5  - 1}}} \right)^2}$

$\Leftrightarrow x = \dfrac{1}{5}\left[ {{{\left( {\dfrac{{27\sqrt 5 }}{{28\sqrt 5  - 1}}} \right)}^2} - 1} \right]\,\,\left( {TM} \right).$

Vậy $x = \dfrac{1}{5}\left[ {{{\left( {\dfrac{{27\sqrt 5 }}{{28\sqrt 5  - 1}}} \right)}^2} - 1} \right]$

Bài 2 (VD):

Phương pháp:

1) Rút gọn $P.$ Thay $x = 16\left( {tmdk} \right)$ vào $P$ để tính toán

2) Rút gọn $Q$ bằng cách trục căn thức ở mẫu rồi tính $Q + \sqrt 2 .$

3) Đánh giá mẫu thức rồi suy ra điều kiện của tử thức

Cách giải:

1) Tính giá trị của biểu thức $P$ khi $x = 16.$

$\begin{array}{l}P = \dfrac{2}{{\sqrt 2  - \sqrt x }} - \dfrac{{\sqrt x  + \sqrt 2 }}{{\sqrt {2x}  - x}}\\ = \dfrac{2}{{\sqrt 2  - \sqrt x }} - \dfrac{{\sqrt x  + \sqrt 2 }}{{\sqrt x \left( {\sqrt 2  - \sqrt x } \right)}}\\ = \dfrac{{2\sqrt x  - \sqrt x  - 2}}{{\sqrt x \left( {\sqrt 2  - \sqrt x } \right)}}\\ = \dfrac{{\sqrt x  - 2}}{{\sqrt x \left( {2 - \sqrt x } \right)}} =  - \dfrac{1}{{\sqrt x }}\end{array}$

Thay $x = 16\,\left( {tmdk} \right)$ vào $P =  - \dfrac{1}{{\sqrt x }}$ ta được :

$P = \dfrac{{ - 1}}{{\sqrt {16} }} =  - \dfrac{1}{4}.$

Vậy với $x = 16$ thì $P =  - \dfrac{1}{4}.$

2) Chứng minh rằng $Q + \sqrt 2  = \sqrt x .$

Ta có:

$Q = \dfrac{1}{{\sqrt x  - \sqrt {x - 1} }} - \dfrac{{x - 3}}{{\sqrt {x - 1}  - \sqrt 2 }}$

$= \dfrac{{\left( {\sqrt x  + \sqrt {x - 1} } \right)}}{{\left( {\sqrt x  - \sqrt {x - 1} } \right)\left( {\sqrt x  + \sqrt {x - 1} } \right)}} - \dfrac{{\left( {x - 3} \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}{{\left( {\sqrt {x - 1}  - \sqrt 2 } \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}$

$= \dfrac{{\sqrt x  + \sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} - \dfrac{{\left( {x - 3} \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}{{\left( {x - 1} \right) - 2}}$

$\begin{array}{l} = \sqrt x  + \sqrt {x - 1}  - \left( {\sqrt {x - 1}  + \sqrt 2 } \right)\\ = \sqrt x  - \sqrt 2 \end{array}$

Từ đó

$Q + \sqrt 2  = \sqrt x  - \sqrt 2  + \sqrt 2  = \sqrt x$

Vậy $Q + \sqrt 2  = \sqrt x .$

3) Tìm $x$ để $P.Q \ge 0.$

Ta có: $P =  - \dfrac{1}{{\sqrt x }};Q = \sqrt x  - \sqrt 2$ với $x > 1;x \ne 2;x \ne 3$

Nên $M = P.Q = \dfrac{{\left( {\sqrt x  - \sqrt 2 } \right) \cdot \left( { - 1} \right)}}{{\sqrt x }} = \dfrac{{\sqrt 2  - \sqrt x }}{{\sqrt x }}$

Để $M \ge 0 \Leftrightarrow \dfrac{{\sqrt 2  - \sqrt x }}{{\sqrt x }} \ge 0$

Với $x > 1$ và $x \ne 2,\,x \ne 3$ thì $\sqrt x  > 0$

Nên $M \ge 0 \Leftrightarrow \dfrac{{\sqrt 2  - \sqrt x }}{{\sqrt x }} \ge 0 \\\Leftrightarrow \sqrt 2  - \sqrt x  \ge 0$

$\Leftrightarrow \sqrt x  \le \sqrt 2  \Leftrightarrow 0 \le x \le 2$

Kết hợp điều kiện $x > 1$ và $x \ne 2,\,x \ne 3$ ta có $1 < x < 2$

Vậy $1 < x < 2$ thỏa mãn yêu cầu bài toán.

Bài 3 (VD ):

Phương pháp:

a) Hai đường thẳng $y = ax + b;y = a'x + b'$ song song với nhau khi $\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$

b) Xét phương trình hoành độ giao điểm rồi biện luận theo $m$ phương trình thu được.

Tìm tung độ giao điểm rồi cho tung độ đó bằng $0.$

Cách giải:

Xét hai hàm số bậc nhất $y = \left( {m + 1} \right)x + 2m$ và $y = \left( {2m + 1} \right)x + 3m$ (ĐK: $m \ne  - 1;\,m \ne \dfrac{{ - 1}}{2}$)

1) Hai đường thẳng song song khi

$\left\{ \begin{array}{l}m + 1 = 2m + 1\\2m \ne 3m\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}m = 0\\m \ne 0\end{array} \right.$

Vậy không tồn tại giá trị của $m$ thỏa mãn đề bài.

2) Để hai đường thẳng cắt nhau tại điểm trên trục hoành. Khi đó ta có

$\Leftrightarrow$ Phương trình hoành độ $\left( {m + 1} \right)x + 2m = \left( {2m + 1} \right)x + 3m \\\Leftrightarrow x.m =  - m$

+) Nếu $m = 0$ thì hai đường thẳng trùng nhau.

+) Khi $m \ne 0$ ta có hoành độ giao điểm là $x =  - 1.$

Với $x =  - 1$ ta có tung độ giao điểm là $y = \left( {m + 1} \right).\left( { - 1} \right) + 2m = m - 1$

Để thỏa mãn đề ta cần có tung độ giao điểm bằng $0.$

$y = 0 \Leftrightarrow m - 1 = 0 \Leftrightarrow m = 1$ (thỏa mãn)

Vậy $m = 1.$

Bài 4 (VD ):

Phương pháp:

1) Chỉ ra $OCED$ là hình vuông

Chu vi tam giác bằng tổng ba cạnh

2) Sử dụng tính chất đường trung bình và tính chất tam giác vuông cân

3) Sử dụng tính chất hai tam giác đồng dạng

4) Sử dụng định lý Pytago và bất đẳng thức Cô-si cho hai số không âm.

Cách giải:

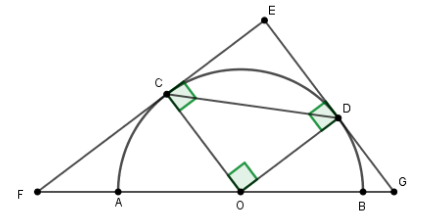
1) Tính chu vi của tam giác $ECD$ theo $R.$

Từ tính chất của tiếp tuyến ta có $\widehat {OCG} = \widehat {ODG} = {90^0} = \widehat {COD}$ nên $CODE$ là chữ nhật.

Lại có $OC = OD = R$ nên $CODE$ là hình vuông.

Suy ra $CE = DE = CO = DO = R$

Xét tam giác $ECD$ vuông tại $E,$ theo định lý Pytago ta có: $CD = \sqrt {C{E^2} + D{E^2}}  = \sqrt {{R^2} + {R^2}}  = R\sqrt 2$

Chu vi tam giác $CED$ là $EC + ED + CD = 2R + R\sqrt 2 .$

2) Khi tứ giác $FCDG$ là hình thang cân. Hãy tính tỉ số $\dfrac{{AB}}{{FG}}.$

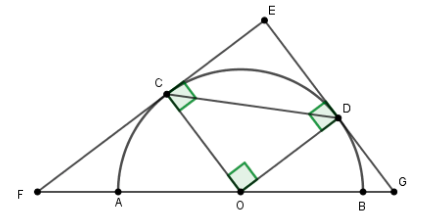
Khi tứ giác $PCDG$ là hình thang cân thì $CF = DG;\widehat F = \widehat G$ và $CD//FG$

Ta có tam giác $EFG$ cân tại $E$ có $\widehat {EFG} = {90^0}$ nên $\widehat F = \widehat G = {45^0}$

Xét tam giác $OFC$ vuông tại $C$ có $\widehat F = {45^0}$ nên tam giác $CFO$ vuông cân tại $C.$

Suy ra $CF = CO = R$

Tương tự ta có $DG = DO = R$

Từ đó $CF = CE = DE = DG = R$ nên $C,D$ lần lượt là trung điểm của $EF,EG$

Suy ra  $CD$ là đường trung bình của tam giác $EFG.$ Khi đó $FG = 2CD = 2R\sqrt 2$

$\Rightarrow \dfrac{{AB}}{{FG}} = \dfrac{{2R}}{{2R\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}$

3) Chứng minh rằng $FC.DG$ luôn là hằng số.

Ta có: $\widehat F = \widehat {DOC}$ (cùng phụ với $\widehat {COF}$)

Nên hai tam giác vuông $FCO$ và $ODG$ đồng dạng (góc-góc)

Ta có : $\dfrac{{CF}}{{OD}} = \dfrac{{CO}}{{DG}} \Leftrightarrow CF.DG = CO.DO = {R^2}$

4) Tìm vị trí của $C,D$ sao cho tích $AD.BC$ đạt giá trị lớn nhất.

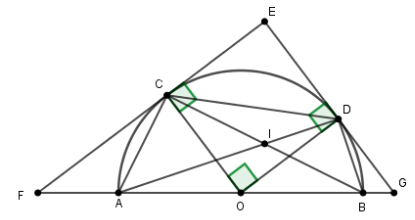
Gọi giao điểm của $CB$ và $AD$ là $I.$ Khi đó ta có các tam giác $ACI,\,BDI$ vuông cân tại $C,D.$

Đặt $AC = x;BD = y \\\Rightarrow CB.AD = \left( {x + y\sqrt 2 } \right)\left( {y + x\sqrt 2 } \right) \\= 3xy + \left( {{x^2} + {y^2}} \right)\sqrt 2 .$

Ta có $A{C^2} + C{B^2} + B{D^2} + A{D^2} = 8{R^2}$ (định lý Pytago)

Suy ra $4\left( {{x^2} + {y^2}} \right) + 4xy\sqrt 2  = 8{R^2}\mathop  \ge \limits^{Co - si} 8xy + 4xy\sqrt 2$ $\Leftrightarrow xy \le \dfrac{{8{R^2}}}{{8 + 4\sqrt 2 }}$ .

Dấu  khi $x = y.$

Ta có $2\sqrt 2 AD.BC - 8{R^2} = 2xy\sqrt 2 .$

Vậy để tích $CB.AD$ lớn nhất thì $x = y$ khi đó $C,D$ là điểm chính giữa của các cung phần tư thứ nhất và thứ hai trên nửa đường tròn đã cho.

Bài 5 (VDC ):

Phương pháp:

Đánh giá và chọn ra bộ số thích hợp để chứng minh không tồn tại giá trị lớn nhất của $T.$

Cách giải:

Với $a > 0$ ta có hệ thức :

$\begin{array}{l}{\left( {1 + \dfrac{1}{a} - \dfrac{1}{{a + 1}}} \right)^2} = 1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}} + \dfrac{2}{a} - \dfrac{2}{{a + 1}} - 2\dfrac{1}{{a\left( {a + 1} \right)}}\\ = 1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}} + \dfrac{2}{a} - \dfrac{2}{{a + 1}} - \dfrac{2}{a} + \dfrac{2}{{a + 1}}\\ = 1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}}\end{array}$

Nên

$\sqrt {1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}}}  = \left| {1 + \dfrac{1}{a} - \dfrac{1}{{a + 1}}} \right| \\= 1 + \dfrac{1}{a} - \dfrac{1}{{a + 1}}$

Khi đó: $T = \sqrt {1 + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{{\left( {x + 1} \right)}^2}}}}  + \sqrt {1 + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{{\left( {y + 1} \right)}^2}}}}  + \dfrac{4}{{\left( {x + 1} \right)\left( {y + 1} \right)}} \\= 2 + \dfrac{1}{x} + \dfrac{1}{y}$

Ta sẽ chứng minh không tồn tại giá trị lớn nhất của $T.$

Giả sử $M > 0$ là giá trị lớn nhất của $T.$

Khi đó nếu ta chọn $\dfrac{1}{x} = M + 1 \Leftrightarrow x = \dfrac{1}{{M + 1}} \in \left( {0;1} \right);\,y = 2 - \dfrac{1}{{M + 1}} > 0$ khi đó ta có $x,y$ vừa chọn thỏa mãn là các số dương và $x + y = 2.$

Với bộ $x,y$ vừa chọn ta có $T = 2 + \dfrac{1}{x} + \dfrac{1}{y} > 2 + M + 1.$

Vậy không tồn tại giá trị lớn nhất của $T.$