Giải đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Hai Bà Trưng — Không quảng cáo

Đề bài

Bài 1  (2 điểm):

Cho hai biểu thức:

$A = \dfrac{{4\sqrt x }}{{\sqrt x  - 5}}$ và $B = \dfrac{{\sqrt x  - 2}}{{\sqrt x  - 1}} + \dfrac{1}{{\sqrt x  + 2}} + \dfrac{{5 - 2\sqrt x }}{{x + \sqrt x  - 2}}$ với $x > 0,x \ne 1,x \ne 25$

1) Tính giá trị của biểu thức A tại x = 9.

2) Rút gọn biểu thức B.

3) Tìm số tự nhiên x lớn nhất sao cho $\dfrac{A}{B} < 4$

Bài 2 (2,5 điểm):

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Theo kế hoạch, trong tháng 3 năm 2020 hai tổ phải may 1500 chiếc khẩu trang để phục vụ cho công tác phòng, chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức 10%; tổ II may vượt mức 12% nên cả hai tổ đã may được 1664 chiếc khẩu trang. Hỏi theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?

2) Một cửa hàng bán xăng dầu dự định đặt làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao 1,8 m, bán kính đáy 0,6 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu? (Bỏ qua bề dầy của bồn)

Bài 3 (1,5 điểm):

Cho Parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 3x + m - 1$

a) Tìm tọa độ giao điểm của đường thẳng (d) và parabol (P) khi m = 5.

b) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn $x_1^3 + x_2^3 = 9$

Bài 4 (3,5 điểm):

Cho đường tròn (O;R), đường kính AB cố định. Gọi M là trung điểm của đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung nhỏ AC (E khác A và C). Nối EB cắt CD tại H, kéo dài AE cắt tia DC tại K.

a) Chứng minh tứ giác BMEK là tứ giác nội tiếp.

b) Chứng minh tam giác AEM đồng dạng với tam giác ABK và $AE.AK = 3{R^2}$

c) Chứng minh tâm I của đường tròn ngoại tiếp tam giác BHK luôn thuộc một đường thẳng cố định khi điểm E chuyển động trên cung nhỏ AC.

Bài 5 (0,5 điểm):

Cho 3 số thực dương x, y, z thỏa điều kiện x + y + z = 3.

Tìm giá trị nhỏ nhất của biểu thức $P = \dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}$

HẾT

LG bài 1

Phương pháp giải:

1) Kiểm tra x = 9 có thỏa mãn điều kiện hay không và thay vào A tính toán.

2) Quy đồng và rút gọn.

3) Rút gọn biểu thức $\dfrac{A}{B}$ rồi cho $\dfrac{A}{B} < 4$ tìm x.

Chú ý kết hợp ĐKXĐ và x là số tự nhiên lớn nhất.

Lời giải chi tiết:

Cho hai biểu thức:

$A = \dfrac{{4\sqrt x }}{{\sqrt x  - 5}}$ và $B = \dfrac{{\sqrt x  - 2}}{{\sqrt x  - 1}} + \dfrac{1}{{\sqrt x  + 2}} + \dfrac{{5 - 2\sqrt x }}{{x + \sqrt x  - 2}}$ với $x > 0,x \ne 1,x \ne 25$

1) Tính giá trị của biểu thức A tại x = 9.

Thay $x = 9$ (TMĐK) vào biểu thức A ta được:

$A = \dfrac{{4\sqrt 9 }}{{\sqrt 9  - 5}} = \dfrac{{4.3}}{{3 - 5}} = \dfrac{{12}}{{ - 2}} =  - 6$

Vậy với x = 9 thì $A =  - 6$.

2) Rút gọn biểu thức B.

Với $x > 0,x \ne 1,x \ne 25$ ta có:

$\begin{array}{l}B = \dfrac{{\sqrt x  - 2}}{{\sqrt x  - 1}} + \dfrac{1}{{\sqrt x  + 2}} + \dfrac{{5 - 2\sqrt x }}{{x + \sqrt x  - 1}}\\ = \dfrac{{\sqrt x  - 2}}{{\sqrt x  - 1}} + \dfrac{1}{{\sqrt x  + 2}} + \dfrac{{5 - 2\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right) + \sqrt x  - 1 + 5 - 2\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{x - 4 + \sqrt x  - 1 + 5 - 2\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{x - \sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{\sqrt x }}{{\sqrt x  + 2}}\end{array}$

Vậy $B = \dfrac{{\sqrt x }}{{\sqrt x  + 2}}$

3) Tìm số tự nhiên x lớn nhất sao cho $\dfrac{A}{B} < 4$

$\begin{array}{l}M = \dfrac{A}{B} = \dfrac{{4\sqrt x }}{{\sqrt x  - 5}}:\dfrac{{\sqrt x }}{{\sqrt x  + 2}}\\ = \dfrac{{4\sqrt x }}{{\sqrt x  - 5}}.\dfrac{{\sqrt x  + 2}}{{\sqrt x }}\\ = \dfrac{{4\left( {\sqrt x  + 2} \right)}}{{\sqrt x  - 5}}\end{array}$

Do đó

$\begin{array}{l}M < 4 \Leftrightarrow \dfrac{{4\left( {\sqrt x  + 2} \right)}}{{\sqrt x  - 5}} < 4\\ \Leftrightarrow \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 5}} < 1 \Leftrightarrow \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 5}} - 1 < 0\\ \Leftrightarrow \dfrac{{\sqrt x  + 2 - \sqrt x  + 5}}{{\sqrt x  - 5}} < 0\\ \Leftrightarrow \dfrac{7}{{\sqrt x  - 5}} < 0\\ \Leftrightarrow \sqrt x  - 5 < 0\left( {do\,7 > 0} \right)\\ \Leftrightarrow \sqrt x  < 5\\ \Leftrightarrow x < 25\end{array}$

Kết hợp với điều kiện $x > 0,x \ne 1,x \ne 25$ ta được $0 < x < 25$ và $x \ne 1$.

Mà x là số tự nhiên lớn nhất nên $x = 24$(TMĐK).

Vậy $x = 24$.

LG bài 2

Phương pháp giải:

1) Phương pháp giải bài toán bằng cách lập hệ phương trình:

- Gọi ẩn và đặt ĐK cho ẩn.

- Biểu diễn các đại lượng đã biết và chưa biết theo ẩn.

- Thiết lập các phương trình từ điều kiện bài cho suy ra hệ phương trình.

- Giải hệ và kết luận.

2) Thể tích hình trụ $V = \pi {R^2}h$, ở đó $R$ là bán kính đáy, $h$ là chiều cao hình trụ.

Lời giải chi tiết:

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Theo kế hoạch, trong tháng 3 năm 2020 hai tổ phải may 1500 chiếc khẩu trang để phục vụ cho công tác phòng, chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức 10%; tổ II may vượt mức 12% nên cả hai tổ đã may được 1664 chiếc khẩu trang. Hỏi theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?

Gọi số khẩu trang theo kế hoạch tổ I may là x (chiếc, $x \in {N^*},x < 1500$)

số khẩu trang theo kế hoạch tổ II may là y (chiếc, $x \in {N^*},y < 1500$)

Hai tổ phải may 1500 chiếc khẩu trang nên $x + y = 1500$ (1)

Tổ I may vượt mức 10% nên thực tế may được $x + 10\% x = x + 0,1x = 1,1x$ (chiếc)

Tổ II may vượt mức 12% nên thực tế may được $y + 12\% y = y + 0,12y = 1,12y$ (chiếc)

Thực tế cả hai tổ may được 1664 chiếc khẩu trang nên $1,2x + 1,12y = 1664$ (2)

Từ (1) và (2) ta có hệ: $\left\{ \begin{array}{l}x + y = 1500\\1,1x + 1,12y = 1664\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,1y = 1650\\1,1x + 1,12y = 1664\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,02y = 14\\x + y = 1500\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 700\\x = 800\end{array} \right.\end{array}$

Vậy theo kế hoạch,

Tổ I phải may 800 chiếc khẩu trang.

Tổ II phải may 700 chiếc khẩu trang.

2) Một cửa hàng bán xăng dầu dự định đặt làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao 1,8 m, bán kính đáy 0,6 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu? (Bỏ qua bề dầy của bồn)

Thể tích bồn chứa hình trụ là:

$V = \pi {R^2}h = \pi .0,{6^2}.1,8 \approx 2,035\left( {{m^3}} \right)$

Đổi $2,035\,{m^3} = 2035\,l$

Vậy chiếc bồn đó chứa đầy được 2035 lít dầu.

Chú ý:

Khi tính toán đến bước cuối $\pi .0,{6^2}.1,8 = 2,03575204...$ thì các em chỉ lấy $2,035$ chứ không lấy $2,036$ vì thể tích của bồn chứa không thể bằng $2,036$ dẫn tới sẽ không chứa được $2036\,l$ dầu.

LG bài 3

Phương pháp giải:

a) Thay $m = 5$ vào phương trình đường thẳng $\left( d \right):y = 3x + m - 1$ rồi xét phương trình hoành độ giao điểm. Sau đó giải phương trình bậc hai thu được.

b) Sử dụng hệ thức Vi-et và đẳng thức $x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)$

Lời giải chi tiết:

Cho Parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 3x + m - 1$

a) Tìm tọa độ giao điểm của đường thẳng (d) và parabol (P) khi m = 5.

Thay $m = 5$ vào phương trình đường thẳng $\left( d \right):y = 3x + m - 1$ ta được $y = 3x + 4$

Xét phương trình hoành độ giao điểm: ${x^2} = 3x + 4$

$\Leftrightarrow {x^2} - 3x - 4 = 0$

Phương trình này có $a - b + c = 1 - \left( { - 3} \right) - 4 = 0$ nên có hai nghiệm $x =  - 1;x = 4$

Với $x =  - 1 \Rightarrow y = 1$

Với $x = 4 \Rightarrow y = {4^2} = 16$

Vậy tọa độ giao điểm cần tìm là $\left( { - 1;1} \right),\left( {4;16} \right)$

b) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn $x_1^3 + x_2^3 = 9$

Xét phương trình hoành độ giao điểm của Parabol $\left( P \right)$ và đường thẳng $\left( d \right)$:

$\begin{array}{l}{x^2} = 3x + m - 1\\ \Leftrightarrow {x^2} - 3x - m + 1 = 0\left( * \right)\end{array}$

Ta có: $\Delta  = {\left( { - 3} \right)^2} - 4.1.\left( { - m + 1} \right)$ $= 4m + 5$

Để $\left( P \right)$ và $\left( d \right)$ cắt nhau tại hai điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt ${x_1},{x_2}$

$\Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta  > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\4m + 5 > 0\end{array} \right.$ $\Leftrightarrow m >  - \dfrac{5}{4}$

Theo hệ thức Vi-et ta có:

$\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} =  - m + 1\end{array} \right.$

Ta có: ${\left( {{x_1} + {x_2}} \right)^3}$ $= x_1^3 + 3x_1^2{x_2} + 3{x_1}x_2^2 + x_2^3$

$\Rightarrow x_1^3 + x_2^3$ $= {\left( {{x_1} + {x_2}} \right)^3} - \left( {3x_1^2{x_2} + 3{x_1}x_2^2} \right)$$= {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)$

Theo đề bài ta có:

$\begin{array}{l}x_1^3 + x_2^3 = 9\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 9\\ \Leftrightarrow {3^3} - 3\left( { - m + 1} \right).3 = 9\\ \Leftrightarrow 9m =  - 9\end{array}$

$\Leftrightarrow m =  - 1$ (thỏa mãn)

Vậy $m =  - 1$ là giá trị cần tìm.

LG bài 4

Phương pháp giải:

a) Sử dụng dấu hiệu nhận biết tứ giác nội tiếp

b) Sử dụng trường hợp đồng dạng góc góc rồi suy ra hệ thức về cạnh tương ứng

c) Lấy $N$ là điểm đối xứng với $A$ qua $M.$ Sau đó chứng minh đường tròn ngoại tiếp tam giác $ABH$ đi qua $N.$ Từ đó suy ra tính chất của tâm đường tròn ngoại tiếp $I.$

Lời giải chi tiết:

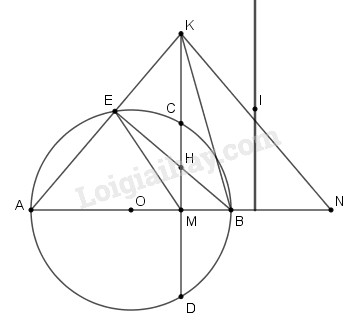
a) Chứng minh tứ giác BMEK là tứ giác nội tiếp.

Xét đường tròn $\left( O \right)$ có $\widehat {AEB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

Suy ra $BE \bot AK \Rightarrow \widehat {BEK} = {90^0}$

Lại có $KD \bot AB \Rightarrow \widehat {KMB} = {90^0}$

Xét tứ giác $BMEK$ có $\widehat {BEK} = \widehat {BMK}\left( { = {{90}^0}} \right)$ nên hai đỉnh $E,M$ kề nhau cùng nhìn cạnh $KB$ dưới một góc vuông, do đó $BMEK$ là tứ giác nội tiếp (dhnb)

b) Chứng minh tam giác AEM đồng dạng với tam giác ABK và $AE.AK = 3{R^2}$

Xét tứ giác nội tiếp $BMEK$ có $\widehat {EKB} = \widehat {EMA}$ (cùng bù với $\widehat {EMB}$)

Xét $\Delta AEM$ và $\Delta ABK$ có:

$\widehat A$ chung

$\widehat {EKB} = \widehat {EMA}$ (chứng minh trên)

Nên $\Delta AEM \backsim \Delta ABK\left( {g - g} \right)$

$\Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AM}}{{AK}}$ $\Leftrightarrow AE.AK = AB.AM$

Mà $AB = 2R,$ $AM = OA + OM$ $= R + \dfrac{1}{2}R = \dfrac{3}{2}R$

Nên $AE.AK = 2R.\dfrac{{3R}}{2}$ $= 3{R^2}$

Vậy $AE.AK = 3{R^2}$

c) Chứng minh tâm I của đường tròn ngoại tiếp tam giác BHK luôn thuộc một đường thẳng cố định khi điểm E chuyển động trên cung nhỏ AC.

Lấy $N$ là điểm đối xứng với $A$ qua $M.$

Suy ra $KM \bot AN,AM = MN$ nên $KM$ là đường trung trực của tam giác $KAN$

Nên $KA = KN \Rightarrow \Delta KAN$ cân tại $K.$

Suy ra $\widehat A = \widehat {KNM}$  (1)

Xét tứ giác $AEHM$ có $\widehat {AEH} + \widehat {HMA}$ $= {90^0} + {90^0} = {180^0}$

Mà hai góc này ở vị trí đối nhau nên $AEHM$ là tứ giác nội tiếp

Suy ra $\widehat A = \widehat {MHB}$ (2) (cùng bù với $\widehat {EHM}$)

Từ (1) và (2) ta có $\widehat {KNB} = \widehat {MHB}$

Xét tứ giác $BHKN$ có $\widehat {KNB} = \widehat {MHB}$ nghĩa là góc ngoài tại đỉnh $H$ bằng góc trong tại đỉnh đối là $N$, do đó $BNKN$ là tứ giác nội tiếp.

Suy ra đường tròn ngoại tiếp tam giác $BHK$ đi qua điểm $N$ cố định (vì $A,M$ cố định)

Vậy tâm đường tròn ngoại tiếp tam giác $BHK$ thuộc đường trung trực của đoạn $BN$ cố định.

LG bài 5

Phương pháp giải:

Sử dụng bất đẳng thức Cô-si cho 2 số không âm $a,b$: $a + b \ge 2\sqrt {ab}$

Dấu “=” xảy ra $\Leftrightarrow a = b$.

Lời giải chi tiết:

Cho 3 số thực dương x, y, z thỏa điều kiện x + y + z = 3.

Tìm giá trị nhỏ nhất của biểu thức $P = \dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}$

Áp dụng bất đẳng thức Cô-si cho 2 số ${y^2},1$ ta có ${y^2} + 1 \ge 2\sqrt {{y^2} + 1}$ $\Leftrightarrow {y^2} + 1 \ge 2y$

Ta có: $\dfrac{x}{{{y^2} + 1}} = \dfrac{{x\left( {{y^2} + 1} \right) - x{y^2}}}{{{y^2} + 1}}$ $= x - \dfrac{{x{y^2}}}{{{y^2} + 1}} \ge x - \dfrac{{x{y^2}}}{{2y}} = x - \dfrac{{xy}}{2}$

Tương tự ta có:

$\dfrac{y}{{{z^2} + 1}} = \dfrac{{y\left( {{z^2} + 1} \right) - y{z^2}}}{{{z^2} + 1}}$ $= y - \dfrac{{y{z^2}}}{{{z^2} + 1}} \ge y - \dfrac{{y{z^2}}}{{2z}} = y - \dfrac{{yz}}{2}$

$\dfrac{z}{{{x^2} + 1}} = \dfrac{{z\left( {{x^2} + 1} \right) - z{x^2}}}{{{x^2} + 1}}$ $= z - \dfrac{{z{x^2}}}{{{x^2} + 1}} \ge z - \dfrac{{z{x^2}}}{{2x}} = z - \dfrac{{zx}}{2}$

Cộng theo từng vế ta được:

$\dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}$ $\ge x + y + z - \dfrac{{xy + yz + xz}}{2}$  (1)

Mặt khác, theo BĐT Cô-si ta có:

$\begin{array}{l}{x^2} + {y^2} \ge 2xy\\{y^2} + {z^2} \ge 2yz\\{x^2} + {z^2} \ge 2xz\end{array}$

Suy ra $2\left( {{x^2} + {y^2} + {z^2}} \right) \ge 2\left( {xy + yz + xz} \right)$

$\Leftrightarrow {x^2} + {y^2} + {z^2} \ge xy + yz + zx$

$\Leftrightarrow {x^2} + {y^2} + {z^2} + 2\left( {xy + yz + xz} \right)$ $\ge 3\left( {xy + yz + xz} \right)$

$\Leftrightarrow {\left( {x + y + z} \right)^2} \ge 3\left( {xy + yz + xz} \right)$

$\Leftrightarrow {3^2} \ge 3\left( {xy + yz + xz} \right)$ $\Leftrightarrow xy + yz + xz \le 3$ (2)

Từ (1) và (2) ta có:  $\dfrac{x}{{{y^2} + 1}} + \dfrac{y}{{{z^2} + 1}} + \dfrac{z}{{{x^2} + 1}}$$\ge 3 - \dfrac{3}{2} = \dfrac{3}{2}$

Hay $P \ge \dfrac{3}{2}$

Dấu “=” xảy ra khi $x = y = z = 1.$

Vậy giá trị nhỏ nhất của $P$ là $\dfrac{3}{2}$ khi $x = y = z = 1.$

HẾT