Giải đề thi kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Cầu Giấy — Không quảng cáo

Câu 1.  (3,0 điểm)

Cho biểu thức $A = \left( {\dfrac{1}{{\sqrt x  + 2}} - \dfrac{1}{{\sqrt x  - 2}}} \right):\dfrac{{\sqrt x }}{{x - 2\sqrt x }}$ với $x > 0,\,x \ne 4.$

a) Chứng minh $A = \dfrac{{ - 4}}{{\sqrt x  + 2}}.$

b) Tìm $x$ biết $A = \dfrac{{ - 2}}{3}.$

c) Cho $x$ là số nguyên, tìm giá trị nhỏ nhất của biểu thức $A.$

Câu 2. (2,5 điểm)

Cho hàm số $y = \left( {m + 1} \right)x + 3\,\,\,\left( d \right)$ ($m$ là tham số, $m \ne  - 1$)

a) Tìm $m$ để hàm số trên là hàm số đồng biến.

b) Khi $m = 2,$ hãy vẽ đồ thị hàm số đó trên mặt phẳng tọa độ $Oxy$ và tính khoảng cách từ $O$ đến đường thẳng $\left( d \right).$

c) Đường thẳng $\left( d \right)$ cắt đường thẳng $y =  - \dfrac{3}{2}x + 3\,\,\left( {d'} \right)$ tại điểm $M.$ Gọi $N$ và $P$ lần lượt là giao điểm của đường thẳng $\left( d \right)$ và $\left( {d'} \right)$ với trục hoành $Ox.$ Tìm $m$ để diện tích tam giác $OMP$ bằng $2$ lần diện tích tam giác $OMN.$

Câu 3. (4 điểm)

1) Một chiếc máy bay bay lên với vận tốc $500km/h.$ Đường bay lên tạo với phương nằm ngang một góc $30^\circ .$ Hỏi sau $6$ phút kể từ lúc cất cánh, máy bay lên cao được bao nhiêu ki-lô-mét theo phương thẳng đứng?

2) Cho nửa đường tròn $\left( {O;R} \right)$ đường kính $AB.$ Vẽ hai tiếp tuyến $Ax,\,By$ với nửa đường tròn đó. Trên tia $Ax$ lấy điểm $M$ sao cho $AM > R.$ Từ $M$ kẻ tiếp tuyến $MC$ với nửa đường tròn $\left( O \right)$ ($C$ là tiếp điểm). Tia $MC$ cắt tia $By$ tại $D.$

a) Chứng minh $MD = MA + BD$ và $\Delta OMD$ vuông.

b) Cho $AM = 2R.$ Tính $BD$ và chu vi tứ giác $ABDM.$

c) Tia $AC$ cắt tia $By$ tại $K.$ Chứng minh $OK \bot BM.$

Câu 4. (0,5 điểm) Giải phương trình

$\sqrt {2020x - 2019}  + 2019x + 2019$$= \sqrt {2019x - 2020}$

----------HẾT----------

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1 (VD):

Phương pháp:

a) Qui đồng, khử mẫu và rút gọn $A$.

b) Giải phương trình $A =  - \dfrac{2}{3}$, sử dụng kết quả rút gọn câu a).

c) Dựa vào điều kiện bài cho và $x \in \mathbb{Z}$ suy ra điều kiện chính xác của $x$, từ đó đánh giá $A$.

Cách giải:

a) Chứng minh $A = \dfrac{{ - 4}}{{\sqrt x  + 2}}.$

$A = \left( {\dfrac{1}{{\sqrt x  + 2}} - \dfrac{1}{{\sqrt x  - 2}}} \right):\dfrac{{\sqrt x }}{{x - 2\sqrt x }}$ ($x > 0,\,x \ne 4.$)

$A = \left( {\dfrac{{\sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} - \dfrac{{\sqrt x  + 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right)$ $:\dfrac{{\sqrt x }}{{x - 2\sqrt x }}$

$A = \dfrac{{\sqrt x  - 2 - \sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\dfrac{{\sqrt x }}{{x - 2\sqrt x }}$

$A = \dfrac{{ - 4}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\dfrac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  - 2} \right)}}$

$A = \dfrac{{ - 4}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} \cdot \dfrac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{{\sqrt x }}$

$A = \dfrac{{ - 4}}{{\sqrt x  + 2}}$

b) Tìm $x$ biết $A = \dfrac{{ - 2}}{3}.$

$A = \dfrac{{ - 2}}{3} \Leftrightarrow \dfrac{{ - 4}}{{\sqrt x  + 2}} = \dfrac{{ - 2}}{3}$

$\Leftrightarrow \sqrt x  + 2 = 6 \Leftrightarrow \sqrt x  = 4$

$\Leftrightarrow x = 16$ (TMĐK).

Vậy $x = 16.$

c) Cho $x$ là số nguyên, tìm giá trị nhỏ nhất của biểu thức $A.$

Ta có $x$ nguyên và $x > 0,\,x \ne 4$ thì $x \ge 1,\,x \ne 4,\,x \in \mathbb{Z}.$

Ta có

$x \ge 1 \Leftrightarrow \sqrt x  \ge 1 \Leftrightarrow \sqrt x  + 2 \ge 3 > 0$ $\Leftrightarrow \dfrac{4}{{\sqrt x  + 2}} \le \dfrac{4}{3} \Leftrightarrow \dfrac{{ - 4}}{{\sqrt x  + 2}} \ge \dfrac{{ - 4}}{3}$ $\Leftrightarrow P \ge \dfrac{{ - 4}}{3}$

Dấu  xảy ra $\Leftrightarrow x = 1.$

Vậy giá trị nhỏ nhất của $P$ là $\dfrac{{ - 4}}{3}$ khi $x = 1.$

Câu 2 (VD):

Phương pháp:

a) Hàm số $y = ax + b$ đồng biến trên $\mathbb{R}$ nếu $a > 0$.

b) Tìm điểm đi qua bằng cách cho lần lượt $x = 0,y = 0$, kẻ đường thẳng đi qua hai điểm đã cho ta được đồ thị.

Sử dụng hệ thức giữa cạnh và đường cao trong tam giác vuông tính khoảng cách.

c) Tìm tọa độ các điểm $M,N,P$.

Lập công thức tính diện tích các tam giác $OMP$ và $OMN$ rồi suy ra phương trình ẩn $m$.

Giải phương trình ẩn $m$ và kết luận.

Cách giải:

a) Tìm $m$ để hàm số trên là hàm số đồng biến.

Hàm số đã cho đồng biến khi $m + 1 > 0$ $\Leftrightarrow m >  - 1$

b) Khi $m = 2,$ hãy vẽ đồ thị hàm số đó trên mặt phẳng tọa độ $Oxy$ và tính khoảng cách từ $O$ đến đường thẳng $\left( d \right).$

Khi $m = 2$ hàm số có dạng $y = 3x + 3$

* Cho $x = 0$ thì $y = 3$

Cho $y = 0$ thì $x =  - 1$

$\Rightarrow$ Đường thẳng đi qua hai điểm $\left( {0;3} \right)$ và $\left( { - 1;0} \right)$ là đồ thị hàm số $y = 3x + 3$

* Vẽ đồ thị hàm số trên mặt phẳng tọa độ.

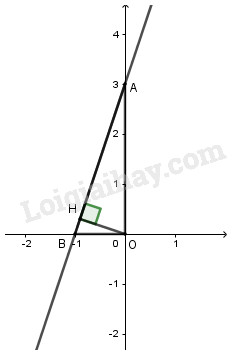
Gọi $A\left( {0;3} \right)$ và $B\left( { - 1;0} \right)$ nên $OA = 3,\,OB = 1.$

Kẻ $OH$ vuông góc với $d$ tại $H.$

Xét tam giác $OAB$ vuông tại $O,$ đường cao $OH$

Có $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{{3^2}}} + \dfrac{1}{{{1^2}}} \Rightarrow O{H^2} = \dfrac{9}{{10}}$

$\Rightarrow OH = \dfrac{{3\sqrt {10} }}{{10}}$

c) Đường thẳng $\left( d \right)$ cắt đường thẳng $y =  - \dfrac{3}{2}x + 3\,\,\left( {d'} \right)$ tại điểm $M.$ Gọi $N$ và $P$ lần lượt là giao điểm của đường thẳng $\left( d \right)$ và $\left( {d'} \right)$ với trục hoành $Ox.$ Tìm $m$ để diện tích tam giác $OMP$ bằng $2$ lần diện tích tam giác $OMN.$

Hai đường thẳng $\left( d \right)$ và $\left( {d'} \right)$ cắt nhau khi và chỉ khi $m + 1 \ne \dfrac{{ - 3}}{2}$ $m \ne \dfrac{{ - 5}}{2}$

Hoành độ giao điểm $M$ của $\left( d \right)$ và $\left( {d'} \right)$ là nghiệm của phương trình

$\left( {m + 1} \right)x + 3 = \dfrac{{ - 3}}{2}x + 3 \Leftrightarrow x = 0$

Mà $y = \dfrac{{ - 3}}{2}x + 3 \Rightarrow y = 3$

$\left( d \right)$ cắt $\left( {d'} \right)$ tại điểm $M\left( {0;3} \right)$

$N$ là giao điểm của $\left( d \right)$ với trục $Ox$ nên $N\left( {\dfrac{{ - 3}}{{m + 1}};0} \right)$

$P$ là giao điểm của $\left( {d'} \right)$ với trục $Ox$ nên $P\left( {2;0} \right)$

Suy ra $ON = \dfrac{3}{{\left| {m + 1} \right|}};\,OP = 2$

Ta có ${S_{OMP}} = 2{S_{OMN}}$ $\Leftrightarrow \dfrac{1}{2}OM.OP = 2 \cdot \dfrac{1}{2} \cdot OM \cdot ON$ $\Leftrightarrow OP = 2ON$

$\Rightarrow 2 = 2 \cdot \dfrac{3}{{\left| {m + 1} \right|}}$ $\Leftrightarrow \left| {m + 1} \right| = 3$ $\left[ \begin{array}{l}m + 1 = 3\\m + 1 =  - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - 4\end{array} \right.$ (TM )

Vậy $m \in \left\{ {2; - 4} \right\}$.

Câu 3 (VD):

Phương pháp:

1) Sử dụng hệ thức lượng trong tam giác vuông, muốn tính cạnh góc vuông ta lấy cạnh huyền nhân với sin góc đối.

2) a) Sử dụng tính chất hai tiếp tuyến cắt nhau.

b) Sử dụng hệ thức lượng trong tam giác vuông ${h^2} = b'c'$ để tính $BD$ .

Chu vi tứ giác bằng tổng các cạnh.

c) - Chứng minh $\Delta AMO$ đồng dạng với $\Delta BAK$.

- Gọi $H$ là giao điểm của $OK$ và $BM$, chứng minh $\widehat {HBO} + \widehat {KOB} = 90^\circ$ suy ra góc $\widehat {OHB} = 90^\circ$.

Cách giải:

1) Một chiếc máy bay bay lên với vận tốc $500km/h.$ Đường bay lên tạo với phương nằm ngang một góc $30^\circ .$ Hỏi sau $6$ phút kể từ lúc cất cánh, máy bay lên cao được bao nhiêu ki-lô-mét theo phương thẳng đứng?

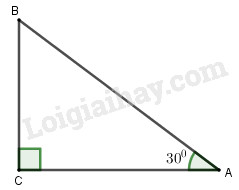
$6$ phút $= 0,1$ giờ.

Gọi $AB$ là đoạn đường máy bay bay lên trong $6$ phút thì $BC$ chính là độ cao máy bay đạt được sau $6$ phút.

Sau $6$ phút máy bay bay được quãng đường là $AB = 500.0,1 = 50km.$

Độ cao của máy bay là $BC = 50.\sin A = 50.\sin 30^\circ  = 25km.$

2) Cho nửa đường tròn $\left( {O;R} \right)$ đường kính $AB.$ Vẽ hai tiếp tuyến $Ax,\,By$ với nửa đường tròn đó. Trên tia $Ax$ lấy điểm $M$ sao cho $AM > R.$ Từ $M$ kẻ tiếp tuyến $MC$ với nửa đường tròn $\left( O \right)$ ( $C$ là tiếp điểm). Tia $MC$ cắt tia $By$ tại $D.$

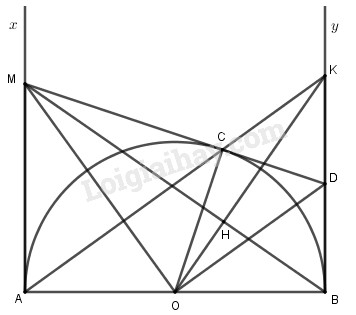
a) Chứng minh $MD = MA + BD$ và $\Delta OMD$ vuông.

Xét $\left( O \right):$ $MA,\,MC$ là $2$ tiếp tuyến cắt nhau tại $M$ với tiếp điểm $A$ và $C$ $\Rightarrow MA = MC.$

$DC,\,DB$ là $2$ tiếp tuyến cắt nhau tại $D$ với tiếp điểm $B$ và $C$ $\Rightarrow DB = DC$

Mà $MD = MC + CD$

$\Rightarrow MD = MA + DB$

Xét $\left( O \right):$

$MA,\,MC$ là $2$ tiếp tuyến cắt nhau tại $M$ với tiếp điểm $A$ và $C$ $\Rightarrow OM$ là tia phân giác của $\widehat {AOC}$

$DC,\,DB$ là $2$ tiếp tuyến cắt nhau tại $D$ với tiếp điểm $B$ và $C$ $\Rightarrow OD$ là tia phân giác của $\widehat {COB}$

Mà $\widehat {AOC}$ và $\widehat {COB}$ là hai góc kề bù

$\Rightarrow OM \bot OD$ tại $D$

$\Rightarrow \widehat {MOD} = 90^\circ$ nên $\Delta OMD$ vuông tại $O.$

b) Cho $AM = 2R.$ Tính $BD$ và chu vi tứ giác $ABDM.$

$AM = 2R \Rightarrow MC = 2R$

Xét tam giác $MOD$ vuông tại $O,$ đường cao $OC,$ có :

$MC.DC = O{M^2}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow 2R.CD = {R^2} \Rightarrow CD = \dfrac{R}{2}$

$\Rightarrow CD = DB = \dfrac{R}{2}$

Do đó chu vi tứ giác $ABDM$ là :

$AB + BD + DM + MA = AB + DB + DC + CM + AM$ $= 2R + \dfrac{R}{2} + \dfrac{R}{2} + 2R + 2R = 7R$

c) Tia $AC$ cắt tia $By$ tại $K.$ Chứng minh $OK \bot BM.$

$\Delta AMO$ đồng dạng với $\Delta BAK$ ($\widehat {MAO} = \widehat {ABK} = 90^\circ ;\,\widehat {AOM} = \widehat {BKA}$ vì cùng phụ với $\widehat {KAB}$)

Suy ra $\dfrac{{AM}}{{AB}} = \dfrac{{AO}}{{BK}} \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{{BO}}{{BK}}$ $\Rightarrow \tan \widehat {MBA} = \tan \widehat {OKB}$ $\Rightarrow \widehat {MBA} = \widehat {OKB}$

Gọi $H$ là giao điểm của $OK$ và $BM$

Ta có $\widehat {MBA} = \widehat {OKB} \Rightarrow \widehat {HBO} = \widehat {OKB}$

Mà $\widehat {OKB} + \widehat {KOB} = 90^\circ$ ($\Delta OBK$ vuông tại $B$)

$\Rightarrow \widehat {HBO} + \widehat {KOB} = 90^\circ$

Hay $\widehat {HBO} + \widehat {HOB} = 90^\circ$$\Rightarrow \widehat {OHB} = 90^\circ$$\Rightarrow OK \bot BM$ tại $H.$

Câu 4 (VDC):

Phương pháp:

- Tìm ĐKXĐ.

- Chuyển vế, nhân chia cho biểu thức liên hợp đưa phương trình về dạng tích.

Cách giải:

ĐK: $x \ge \dfrac{{2020}}{{2019}}$

$\sqrt {2020x - 2019}  + 2019x + 2019$$= \sqrt {2019x - 2020}$

$\Leftrightarrow \sqrt {2020x - 2019}  - \sqrt {2019x - 2020}$$=  - 2019\left( {x + 1} \right)$

$\Leftrightarrow 2020x - 2019 - 2019x + 2020$$=  - 2019\left( {x + 1} \right)\left( {\sqrt {2020x - 2019}  + \sqrt {2019x - 2020} } \right)$

$\Leftrightarrow \left( {x + 1} \right)\left[ {1 + 2019\left( {\sqrt {2002x - 2019}  + \sqrt {2019x - 2020} } \right)} \right] = 0$

Suy ra $x =  - 1$ (không thỏa mãn điều kiện)

Vậy phương trình đã cho vô nghiệm.

HẾT