Giải mục 1 trang 66, 67 SGK Toán 8 - Cùng khám phá
Vẽ tam giác \(ABC\) và một điểm \(O\) bất kì.
Hoạt động 1
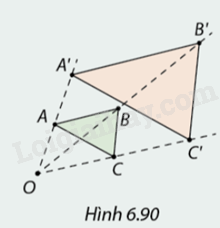
Vẽ tam giác \(ABC\) và một điểm \(O\) bất kì. Trên các tia \(OA,OB,OC,\) chọn các điểm \(A',B',C'\) sao cho \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 2\) (Hình 6.90).
a) Các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\) bằng bao nhiêu? Các cặp cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không?
b) Em có nhận xét gì về tam giác \(ABC\) và tam giác \(A'B'C'\)?
Phương pháp giải:
Xác định các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\), dựa vào tính chất đường trung bình của tam giác xác định các cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không. Sau đó nhận xét về tam giác \(ABC\) và tam giác \(A'B'C'\).
Lời giải chi tiết:
a) Xét tam giác \(OA'C'\), ta có:
\(\frac{{OA'}}{{OC'}} = 2\)
=> A là trung điểm của \(OA'\)
\(\frac{{OC'}}{{OC}} = 2\)
=> C là trung điểm của \(OC'\).
=> AC là đường trung bình của tam giác \(OA'C'\).
Áp dụng tính chất đường trung bình của tam giác ta có: \(\frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Chứng minh tương tự với tam giác \(OA'B';OB'C'\)
Ta được tỉ số: \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Các cặp cạnh \(AB//A'B';BC//B'C';AC//A'C'\).
b) Vì \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\), ta được \(\Delta ABC\) ∽ \(\Delta A'B'C'\) (cạnh-cạnh-cạnh).
Luyện tập 1
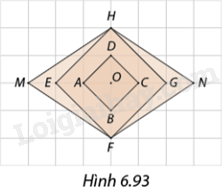
Trong Hình 6.93, tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và theo tỉ số là bao nhiêu?
Phương pháp giải:
Dựa vào tỉ số bằng nhau xác định tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và tỉ số là bao nhiêu.
Lời giải chi tiết:
Tứ giác \(EHGD\) là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) với tỉ số là:
\(\frac{{OE}}{{OA}} = \frac{{OH}}{{OD}} = \frac{{ON}}{{OG}} = \frac{{OF}}{{OB}} = 2\).