Giải mục 1 trang 47 SGK Toán 8 - Cùng khám phá — Không quảng cáo

Hoạt động 1

Cho phân thức $\frac{{{x^2} - 1}}{{x + 2}}$ và $\frac{{2 - x}}{x}$ . Hãy nhân tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức mới.

Phương pháp giải:

Sử dụng phép nhân đa thức với đa thức để nhân tử với tử mẫu với mẫu của 2 đa thức này.

Lời giải chi tiết:

$\left( {{x^2} - 1} \right).\left( {2 - x} \right) = {x^2}\left( {2 - x} \right) - 1\left( {2 - x} \right) = 2{x^2} - {x^3} - 2 + x$

$\left( {x + 2} \right).x = {x^2} + 2x$

Vậy đa thức mới là: $\frac{{2{x^2} - {x^3} - 2 + x}}{{{x^2} + 2x}}$.

Luyện tập 1

Tính tích của hai phân thức $\frac{{{x^2} - 4x + 4}}{{y - x}}$ và $\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}$

Phương pháp giải:

Muốn nhân hai phân thức, ta nhân các tử thức với nhau và các mẫu thức với nhau.

Lời giải chi tiết:

$\begin{array}{l}\frac{{{x^2} - 4x + 4}}{{y - x}}.\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{\left( {{x^2} - 4x + 4} \right).{{\left( {x - y} \right)}^2}}}{{\left( {y - x} \right).3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{{{\left( {x - 2} \right)}^2}.{{\left( {x - y} \right)}^2}}}{{ - \left( {x - y} \right).3{{\left( {x - 2} \right)}^2}}}\\ = \frac{{x - y}}{{ - 3}}\end{array}$

Vận dụng 1

Tính diện tích của hình chữ nhật trong Hình 2.3 theo x.

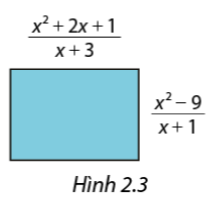
Phương pháp giải:

Áp dụng công thức tính diện tích hình chữ nhật để tính diện tích hình trên theo x.

Lời giải chi tiết:

Diện tích của hình chữ nhật trên là:

$\begin{array}{l}S = \frac{{{x^2} + 2x + 1}}{{x + 3}}.\frac{{{x^2} - 9}}{{x + 1}} = \frac{{\left( {{x^2} + 2x + 1} \right).\left( {{x^2} - 9} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \frac{{{{\left( {x + 1} \right)}^2}.\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \left( {x + 1} \right)\left( {x - 3} \right)\\ = x\left( {x - 3} \right) + 1\left( {x - 3} \right) = {x^2} - 3x + x - 3 = {x^2} - 2x - 3\end{array}$

Luyện tập 2

Tính nhanh: $\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}$

Phương pháp giải:

Sử dụng các hằng đẳng thức đáng nhớ và phương pháp nhân hai phân thức để tính nhanh.

Lời giải chi tiết:

$\begin{array}{l}\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\\ = \frac{{\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}.{x^2}.{{\left( {x - y} \right)}^2}}}{{{x^2}{{\left( {x - y} \right)}^2}.\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}}}\\ = 1\end{array}$