Giải mục 1 trang 82, 83 SGK Toán 11 tập 2 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 1

Cho đường thẳng $a$ và mặt phẳng $\left( P \right)$.

a) Trong trường hợp $a$ vuông góc với $\left( P \right)$, tìm góc giữa $a$ và một đường thẳng $b$ tuỳ ý trong $\left( P \right)$.

b) Trong trường hợp $a$ không vuông góc với $\left( P \right)$, tìm góc giữa $a$ và đường thẳng $a'$ là hình chiếu vuông góc của $a$ trên $\left( P \right)$.

Phương pháp giải:

Sử dụng tính chất: Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng.

Lời giải chi tiết:

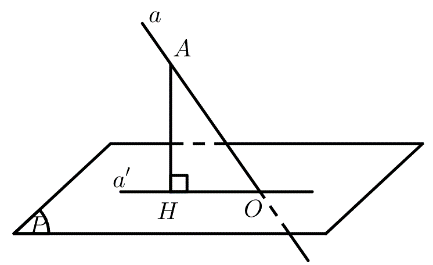
a) Ta có:

$\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^ \circ }$

b) Lấy $A \in a$. Gọi $O = a \cap \left( P \right)$. Dựng $AH \bot a'\left( {H \in a'} \right)$.

Ta có: $\left( {a,a'} \right) = \left( {AO,OH} \right) = \widehat {AOH}$

Thực hành 1

Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa các đường thẳng sau đây với mặt phẳng $\left( {ABCD} \right)$:

a) $AA'$;

b) $BC'$;

c) $A'C$.

Phương pháp giải:

Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải chi tiết:

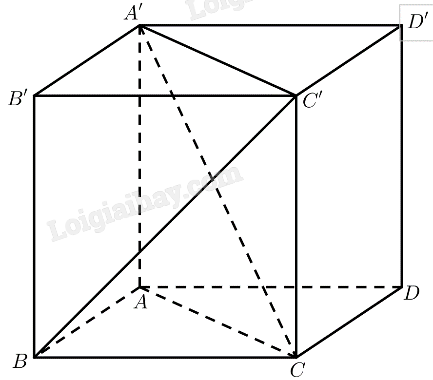
a) $AA' \bot \left( {ABCD} \right) \Rightarrow \left( {AA',\left( {ABCD} \right)} \right) = {90^ \circ }$.

b) $CC' \bot \left( {ABCD} \right)$

$\Rightarrow \left( {BC',\left( {ABCD} \right)} \right) = \left( {BC',BC} \right) = \widehat {CBC'} = {45^ \circ }$

c) $AA' \bot \left( {ABCD} \right)$

$\Rightarrow \left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {ACA'}$

$\begin{array}{l}AC = AB\sqrt 2  = AA'\sqrt 2  \Rightarrow \tan \widehat {ACA'} = \frac{{AA'}}{{AC}} = \frac{{AA'}}{{AA'\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat {ACA'} \approx 35,{26^ \circ }\end{array}$

Vậy $\left( {A'C,\left( {ABCD} \right)} \right) \approx 35,{26^ \circ }$

Vận dụng 1

Một tấm ván hình chữ nhật $ABCD$ được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết $AB = 1\,m,AD = 3,5{\rm{ }}m$. Tính góc giữa đường thẳng $BD$ và đáy hồ.

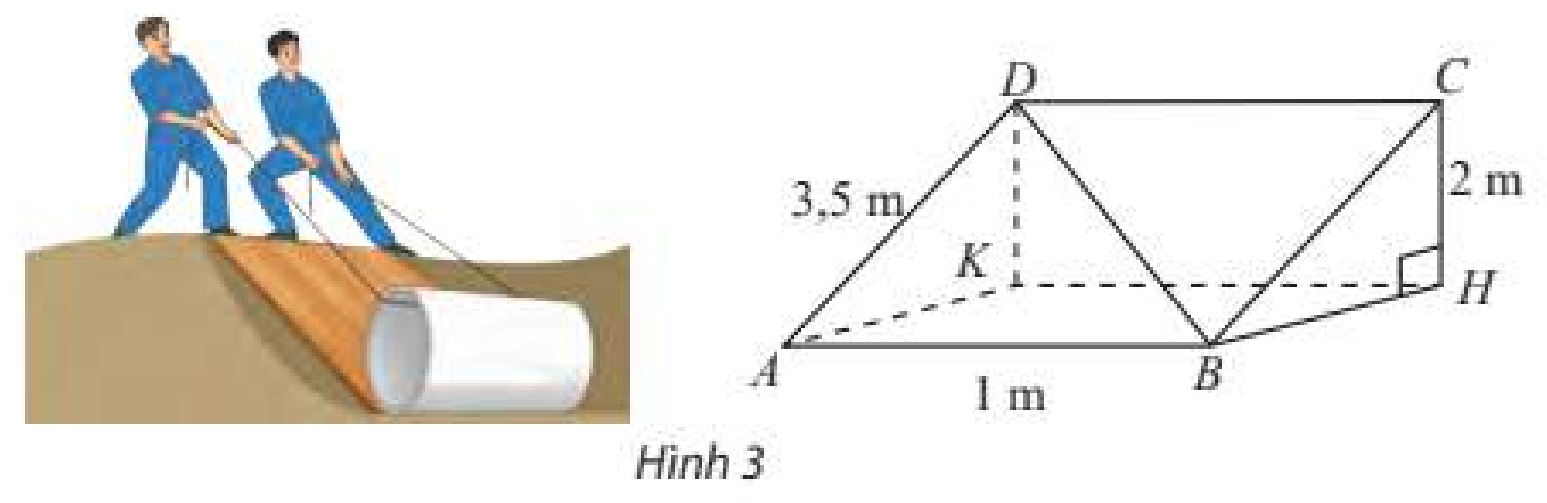
Phương pháp giải:

Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải chi tiết:

$DK \bot \left( {ABHK} \right) \Rightarrow \left( {B{\rm{D}},\left( {ABHK} \right)} \right) = \left( {B{\rm{D}},BK} \right) = \widehat {DBK}$

$DK = CH = 2,AK = \sqrt {A{{\rm{D}}^2} - D{K^2}}  = \frac{{\sqrt {33} }}{2},KB = \sqrt {A{K^2} + A{B^2}}  = \frac{{\sqrt {37} }}{2}$

$\tan \widehat {DBK} = \frac{{DK}}{{KB}} = \frac{4}{{\sqrt {37} }} \Rightarrow \widehat {DBK} \approx 33,{3^ \circ }$

Vậy góc giữa đường thẳng $BD$ và đáy hồ bằng $33,{3^ \circ }$.