Giải mục 2 trang 26, 27, 28, 29, 30 SGK Toán 12 tập 2 - Cùng khám phá
Trong không gian Oxyz, cho một khối nón có đỉnh \(O\), chiều cao bằng 8, bán kính đáy bằng 3, và có trục trùng với Ox. Khi cắt khối nón bởi mặt phẳng vuông góc với trục Ox tại điểm \(x\) (\(0 \le x \le 8\)) thì phần chung giữa mặt phẳng và khối nón là một hình tròn có diện tích \(S(x)\) thay đổi theo \(x\) (Hình 4.19) (khối nón là phần không gian được giới hạn bởi một hình nón kể cả hình nón đó).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 26 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho một khối nón có đỉnh \(O\), chiều cao bằng 8, bán kính đáy bằng 3, và có trục trùng với Ox. Khi cắt khối nón bởi mặt phẳng vuông góc với trục Ox tại điểm \(x\) (\(0 \le x \le 8\)) thì phần chung giữa mặt phẳng và khối nón là một hình tròn có diện tích \(S(x)\) thay đổi theo \(x\) (Hình 4.19) (khối nón là phần không gian được giới hạn bởi một hình nón kể cả hình nón đó).
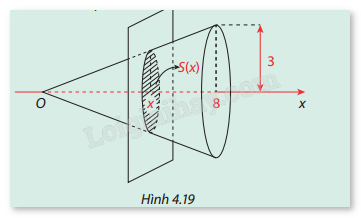
a) Tính thể tích của khối nón.
b) Viết biểu thức tính \(S(x)\).
c) Tính \(\int_0^8 S (x){\mkern 1mu} dx\) và rút ra nhận xét.
Phương pháp giải:
a) Sử dụng công thức tính thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h\).
b) Tìm bán kính tại điểm \(x\) và từ đó suy ra biểu thức tính \(S(x)\).
c) Tính thể tích bằng cách lấy tích phân của diện tích thiết diện theo \(x\).
Lời giải chi tiết:
a)
Công thức tính thể tích khối nón là:
\(V = \frac{1}{3}\pi {r^2}h\)
Trong đó, \(r = 3\) và \(h = 8\). Vậy:
\(V = \frac{1}{3}\pi ({3^2})(8) = \frac{1}{3}\pi (9)(8) = 24\pi \)
Vậy thể tích của khối nón là \(24\pi \).
b)
Bán kính tại điểm \(x\) có thể tính từ tỉ lệ:
\(\frac{{r(x)}}{x} = \frac{3}{8}\)
Suy ra:
\(r(x) = \frac{{3x}}{8}\)
Diện tích thiết diện là:
\(S(x) = \pi r{(x)^2} = \pi {\left( {\frac{{3x}}{8}} \right)^2} = \frac{{9\pi {x^2}}}{{64}}\)
c)
Tính thể tích bằng cách lấy tích phân của diện tích thiết diện theo \(x\):
\(V = \int_0^8 S (x){\mkern 1mu} dx = \int_0^8 {\frac{{9\pi {x^2}}}{{64}}} {\mkern 1mu} dx\)
Tính tích phân:
\(V = \frac{{9\pi }}{{64}}\int_0^8 {{x^2}} {\mkern 1mu} dx = \frac{{9\pi }}{{64}}\left[ {\frac{{{x^3}}}{3}} \right]_0^8 = \frac{{9\pi }}{{64}} \cdot \frac{{{8^3}}}{3} = \frac{{9\pi }}{{64}} \cdot \frac{{512}}{3}\)
\(V = \frac{{9\pi \cdot 512}}{{64 \cdot 3}} = \frac{{4608\pi }}{{192}} = 24\pi \)
Vậy kết quả tích phân là \(24\pi \), khớp với thể tích tính theo công thức chuẩn.
LT3
Trả lời câu hỏi Luyện tập 3 trang 28 SGK Toán 12 Cùng khám phá
Bằng tích phân, tính thể tích của khối chóp có diện tích đáy bằng S và chiều cao h.
Phương pháp giải:
- Xác định hệ trục toạ độ.
- Tìm biểu thức diện tích của các mặt cắt ngang.
- Thiết lập tích phân tính thể tích.
Lời giải chi tiết:
Đặt hệ trục sao cho đáy của khối chóp nằm trên mặt phẳng \(z = 0\) và đỉnh khối chóp nằm trên trục \(z\), tại điểm \((0,0,h)\).
Mỗi mặt cắt ngang song song với đáy tại một độ cao \(z\) tạo thành một hình đồng dạng với đáy. Diện tích của mặt cắt tại độ cao \(z\), ký hiệu là \(S(z)\), tỷ lệ với bình phương của tỷ lệ giữa khoảng cách từ mặt cắt đó đến đỉnh và tổng chiều cao \(h\). Ta có:
\(S(z) = {S_0}{\left( {\frac{{h - z}}{h}} \right)^2}\)
với \({S_0}\) là diện tích đáy.
Thể tích của khối chóp bằng tổng diện tích các mặt cắt ngang theo chiều cao \(z\) từ 0 đến \(h\). Công thức tính thể tích là:
\(V = \int_0^h S (z){\mkern 1mu} dz\)
Thay \(S(z) = {S_0}{\left( {\frac{{h - z}}{h}} \right)^2}\) vào:
\(V = \int_0^h {{S_0}} {\left( {\frac{{h - z}}{h}} \right)^2}dz\)
Đặt \(u = \frac{{h - z}}{h}\), suy ra \(du = - \frac{1}{h}dz\). Giới hạn tích phân thay đổi: khi \(z = 0\), \(u = 1\), và khi \(z = h\), \(u = 0\). Tích phân trở thành:
\(V = {S_0}h\int_0^1 {{u^2}} du\)
Tính tích phân:
\(\int_0^1 {{u^2}} {\mkern 1mu} du = \left[ {\frac{{{u^3}}}{3}} \right]_0^1 = \frac{1}{3}\)
Thể tích của khối chóp là:
\(V = {S_0}h \times \frac{1}{3} = \frac{1}{3}{S_0}h\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 28 SGK Toán 12 Cùng khám phá
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \(x = 2\) và \(x = 4\), biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x{\mkern 1mu} (2 \le x \le 4)\) thì phần chung giữa mặt phẳng và vật thể là một hình vuông có độ dài cạnh bằng \(\sqrt {{x^2} - 2} \).
Phương pháp giải:
Để tính thể tích của phần vật thể bị giới hạn bởi hai mặt phẳng \(x = 2\) và \(x = 4\), ta sử dụng phương pháp tích phân thể tích theo mặt cắt ngang. Mặt cắt tại mỗi \(x\) là một hình vuông có cạnh phụ thuộc vào \(x\). Thể tích của vật thể sẽ bằng tích phân diện tích của các mặt cắt đó dọc theo trục \(x\).
Lời giải chi tiết:
Diện tích mặt cắt tại vị trí \(x\) là diện tích hình vuông có cạnh \(\sqrt {{x^2} - 2} \).
Diện tích của mặt cắt này là:
\(A(x) = {\left( {\sqrt {{x^2} - 2} } \right)^2} = {x^2} - 2\)
Thể tích của vật thể là tích phân diện tích các mặt cắt theo \(x\) từ \(x = 2\) đến \(x = 4\):
\(V = \int_2^4 A (x){\mkern 1mu} dx = \int_2^4 {\left( {{x^2} - 2} \right)} {\mkern 1mu} dx\)
Chia tích phân thành hai phần:
\(V = \int_2^4 {{x^2}} {\mkern 1mu} dx - \int_2^4 2 {\mkern 1mu} dx\)
Tính từng tích phân:
- Tích phân của \({x^2}\):
\(\int_2^4 {{x^2}} {\mkern 1mu} dx = \left[ {\frac{{{x^3}}}{3}} \right]_2^4 = \frac{{{4^3}}}{3} - \frac{{{2^3}}}{3} = \frac{{64}}{3} - \frac{8}{3} = \frac{{56}}{3}\)
- Tích phân của \(2\):
\(\int_2^4 2 {\mkern 1mu} dx = 2 \times (4 - 2) = 4\)
Vậy thể tích của phần vật thể là:
\(V = \frac{{56}}{3} - 4 = \frac{{56}}{3} - \frac{{12}}{3} = \frac{{44}}{3}\)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 29 SGK Toán 12 Cùng khám phá
Gọi \((H)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) liên tục và không âm trên đoạn \([a,b]\), trục hoành và các đường thẳng \(x = a\), \(x = b\). Quay \((H)\) xung quanh trục Ox tạo thành một khối tròn xoay (Hình 4.23). Khi cắt khối tròn xoay bởi mặt phẳng vuông góc với trục Ox tại điểm \(x \in [a,b]\), thì phần chung giữa mặt phẳng và khối tròn xoay là một hình tròn bán kính \(f(x)\). Viết công thức tính diện tích hình tròn này, từ đó suy ra công thức tính thể tích của khối tròn xoay tạo thành.
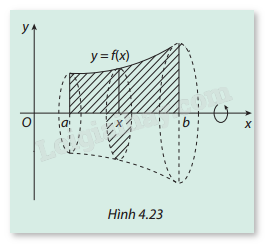
Phương pháp giải:
- Sử dụng công thức tính diện tích hình tròn để tính diện tích của mặt cắt: \(S = \pi {r^2}\).
- Thể tích của khối tròn xoay được tính bằng cách tích phân diện tích các mặt cắt từ \(x = a\) đến \(x = b\).
Lời giải chi tiết:
- Với mỗi \(x \in [a,b]\), diện tích của mặt cắt là diện tích hình tròn có bán kính \(f(x)\):
\(A(x) = \pi \cdot {(f(x))^2}\)
- Thể tích của khối tròn xoay được tính bằng tích phân diện tích của các mặt cắt theo \(x\):
\(V = \int_a^b A (x){\mkern 1mu} dx = \int_a^b \pi \cdot {(f(x))^2}{\mkern 1mu} dx\)
- Đưa \(\pi \) ra ngoài tích phân:
\(V = \pi \int_a^b {(f(} x){)^2}{\mkern 1mu} dx\)
- Công thức tổng quát tính thể tích của khối tròn xoay quanh trục Ox, được tạo ra khi quay hình phẳng giới hạn bởi hàm số \(y = f(x)\) trên đoạn \([a,b]\), là:
\(V = \pi \int_a^b {(f(} x){)^2}{\mkern 1mu} dx\)
LT5
Trả lời câu hỏi Luyện tập 5 trang 29 SGK Toán 12 Cùng khám phá
Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x - 1\), \(y = 0\), \(x = 1\), \(x = 4\).
Phương pháp giải:
Để tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x - 1\), \(y = 0\), \(x = 1\), \(x = 4\) quanh trục Ox, ta sẽ sử dụng phương pháp tính thể tích của khối tròn xoay quanh trục Ox.
Lời giải chi tiết:
Áp dụng công thức tổng quát tính thể tích của khối tròn xoay quanh trục Ox, ta có:
\(V = \int_1^4 {\pi \cdot {{\left( {\sqrt x - 1} \right)}^2}} = \int_1^4 {\pi \cdot \left( {x - 2\sqrt x + 1} \right)} \)
Ta tính từng tích phân riêng lẻ:
\(\int_1^4 x {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2}} \right]_1^4 = \frac{{15}}{2}\)
\(\int_1^4 2 \sqrt x {\mkern 1mu} dx = 2 \cdot \left[ {\frac{2}{3}{x^{3/2}}} \right]_1^4 = \frac{{28}}{3}\)
\(\int_1^4 1 {\mkern 1mu} dx = 4 - 1 = 3\)
Thể tích khối tròn xoay là:
\(V = \pi \left( {\frac{{15}}{2} - \frac{{28}}{3} + 3} \right) = \frac{7}{6}\pi \).
VD2
Trả lời câu hỏi Vận dụng 2 trang 30 SGK Toán 12 Cùng khám phá
Một thùng rượu vang có dạng khối tròn xoay với bán kính mặt đáy và mặt ở trên là 33 cm, bán kính mặt cắt ở chính giữa thùng là 43 cm. Chiều cao của thùng rượu là 112 cm, bao gồm phần thân thùng rượu, hai đế đỡ thùng rượu (mỗi đế cao 3 cm) và thùng rượu được ghép từ các thanh gỗ sồi với độ dày mỗi thanh gỗ là 3 cm (Hình 4.25a và Hình 4.25b). Hình 4.25c mô phỏng phần bên trong thùng rượu có dạng một khối tròn xoay tạo thành khi quay một phần của parabo \((P):y = a{x^2} + bx + c\) quanh trục hoành.
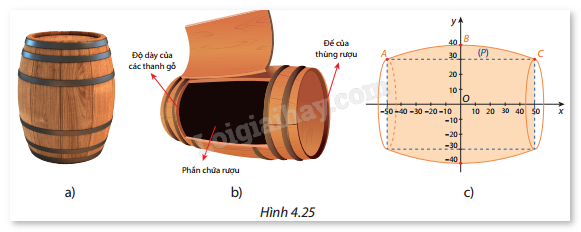
a) Tìm \(a\), \(b\), \(c\).
b) Hỏi thùng rượu chứa được tối đa bao nhiêu lít rượu?
Phương pháp giải:
a) Xác định phương trình parabola từ các điều kiện:
- \(y(0) = 40\)
- \(y(50) = 30\)
b) Tính thể tích khối tròn xoay từ công thức tích phân:
\(V = \pi \int_{ - 50}^{50} {{{\left( {f(x)} \right)}^2}} dx\)
Chuyển kết quả sang đơn vị lít.
Lời giải chi tiết:
a) Tìm \(a\), \(b\), \(c\):
- Phương trình parabola có dạng: \(y = a{x^2} + bx + c\).
- Dựa vào các điều kiện:
\(y(0) = 40\quad \Rightarrow \quad c = 40\)
\(y(50) = 30\quad \Rightarrow \quad a{(50)^2} + b(50) + 40 = 30\)
\(2500a + 50b = - 10\quad (1)\)
\(y( - 50) = 30\quad \Rightarrow \quad 2500a - 50b = - 10\quad (2)\)
- Giải hệ phương trình (1) và (2) cho \(a\) và \(b\):
\(a = \frac{{ - 1}}{{250}},\quad b = 0\)
- Vậy phương trình của parabol là:
\(y = \frac{{ - 1}}{{250}}{x^2} + 40\)
b) Tính thể tích:
- Công thức thể tích:
\(V = 2\pi \int_0^{50} {{{\left( { - \frac{1}{{250}}{x^2} + 40} \right)}^2}} dx\)
- Áp dụng hằng đẳng thức:
\({\left( { - \frac{1}{{250}}{x^2} + 40} \right)^2} = \frac{1}{{62500}}{x^4} - \frac{8}{{25}}{x^2} + 1600\)
- Tính các tích phân:
\(\int_0^{50} {{x^4}} {\mkern 1mu} dx = 62500000,\quad \int_0^{50} {{x^2}} {\mkern 1mu} dx = \frac{{125000}}{3},\quad \int_0^{50} 1 {\mkern 1mu} dx = 50\)
- Thể tích:
\(V = 2\pi \left( {\frac{1}{{62500}}.62500000 - \frac{8}{{25}} \cdot \frac{{125000}}{3} + 1600.50} \right) = \frac{{406000}}{3}{\mkern 1mu} \pi {\rm{c}}{{\rm{m}}^3}\)
- Đổi sang lít:
\(V = \frac{{406}}{3}\pi {\mkern 1mu} ({\rm{lít}})\)
Vậy thùng chứa được khoảng \(425,16\) lít rượu.