Giải mục 2 trang 52, 53, 54 SGK Toán 12 tập 1 - Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng: - Độ dài của vectơ. - Giá của vectơ. - Hai vectơ cùng phương, hai vectơ cùng hướng. - Hai vectơ bằng nhau. - Hai vectơ đối nhau. - Vectơ-không.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 52 SGK Toán 12 Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.
Phương pháp giải:
Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.
Lời giải chi tiết:
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
LT2
Trả lời câu hỏi Luyện tập 2 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).
Phương pháp giải:
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết:
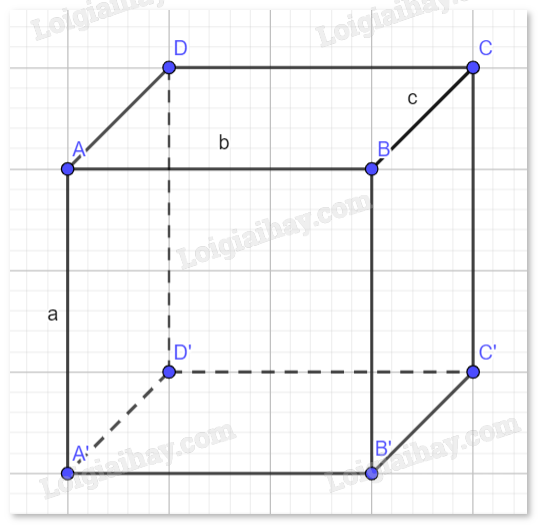
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA'C'\) vuông tại \(A'\). Từ đó ta có:
\(\begin{array}{l}AC' = \sqrt {{{(AA')}^2} + {{(A'C')}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC' = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)