Giải mục 2 trang 38, 39, 40 SGK Toán 8 - Cùng khám phá — Không quảng cáo

Hoạt động 2

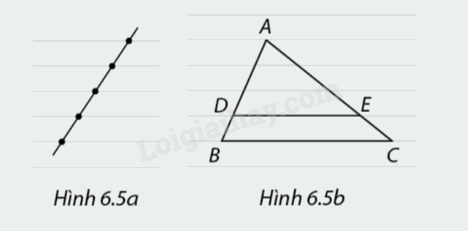
Giấy vở học sinh có các đường kẻ song song và cách đều nhau. Khi vẽ một đường thẳng bất kì cắt các đường kẻ, ta được các đoạn thẳng liên tiếp bằng nhau (Hình 6.5a). Xét $\Delta ABC$ trong hình 6.5b.

1. Chọn $BD$ làm đơn vị đo độ dài, em hãy tính độ dài $AD,AB$ và các tỉ số $\frac{{DA}}{{DB}},\frac{{AD}}{{AB}},\frac{{BD}}{{BA}}.$

2. Chọn $CE$ làm đơn vị đo độ dài, em hãy tính độ dài $AE,AC$ và các tỉ số $\frac{{EA}}{{EC}},\frac{{AE}}{{AC}},\frac{{CE}}{{CA}}.$

3. So sánh các cặp tỉ số$\frac{{DA}}{{DB}}$ và $\frac{{EA}}{{EC}},\frac{{AD}}{{AB}}$ và $\frac{{AE}}{{AC}},\frac{{BD}}{{BA}}$ và $\frac{{CE}}{{CA}}.$ Em có nhận xét gì về các cặp đoạn thẳng được cho?

Phương pháp giải:

Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu $\frac{{AB}}{{CD}}$.

Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức $\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}$ hay $\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}$.

Lời giải chi tiết:

1. Chọn $BD$ là đơn vị đo độ dài, ta có:

$AD = 3\left( {BD} \right)$

$AB = 4\left( {BD} \right)$

$\begin{array}{l}\frac{{DA}}{{DB}} = \frac{3}{1} = 3\\\frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{1}{4} = 0,25\end{array}$

2. Chọn $CE$ làm đơn vị đo độ dài, ta có:

$\begin{array}{l}AE = 3\left( {CE} \right)\\AC = 4\left( {CE} \right)\end{array}$

$\begin{array}{l}\frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{3}{4} = 0,75\\\frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}$

3. Dựa vào tỉ số của các cặp ta thấy các cặp có tỉ số bằng nhau:

$\begin{array}{l}\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}$

Luyện tập 2

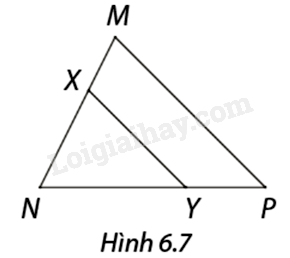
Trong hình 6.7, $XY$ song song với $MP.$ Em hãy cho biết tên đoạn thẳng ở các ô?.

$\frac{{MX}}{{NX}} = \frac{?}{?};\frac{{NY}}{?} = \frac{?}{{MN}}.$

Phương pháp giải:

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

$\begin{array}{l}\frac{{MX}}{{NX}} = \frac{{PY}}{{NY}};\\\frac{{NY}}{{NP}} = \frac{{NX}}{{MN}}\end{array}$

Luyện tập 3

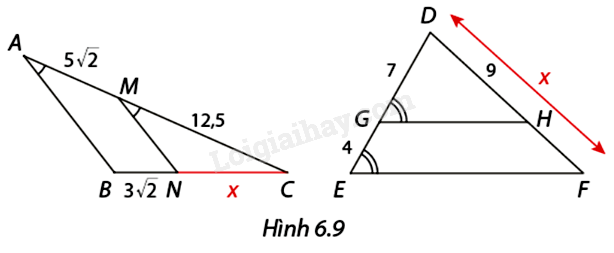
Tính độ dài $x$ trong mỗi trường hợp ở Hình 6.9.

Phương pháp giải:

Dựa vào Định lý Thales thuận và tỉ số của hai đoạn thẳng để tính độ dài x.

Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức $\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}$ hay $\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}$.

Lời giải chi tiết:

Xét tam giác $ABC$, ta có:

$\begin{array}{l}\frac{{MA}}{{MC}} = \frac{{NB}}{{NC}}\\ \Leftrightarrow \frac{{5\sqrt 2 }}{{12,5}} = \frac{{3\sqrt 2 }}{x}\\ \Leftrightarrow x = 7,5\end{array}$

Xét tam giác $DEF$, ta có:

$\begin{array}{l}\frac{{DG}}{{DE}} = \frac{{DH}}{{DF}}\\ \Leftrightarrow \frac{7}{{11}} = \frac{9}{x}\\ \Leftrightarrow x = \frac{{99}}{7}\end{array}$

Vận dụng 1

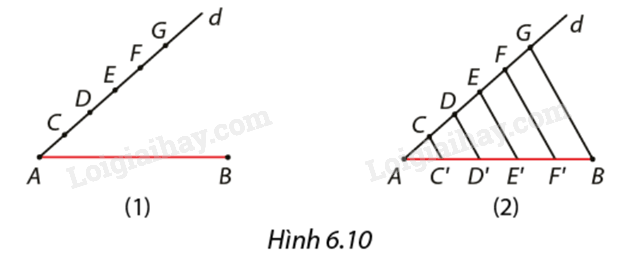
Để chia đoạn thẳng $AB$ thành năm phần bằng nhau, An làm như sau (Hình 6.10):

1. Vẽ đường thẳng $d$ di qua $A$ không trùng với $AB.$ Trên $d$ lấy năm điểm $C,D,E,F,G$ sao cho $AC = CD = DE = {\rm{EF = FG;}}$

2. Vẽ các đường thẳng đi qua $C,D,E,F$ song song với đường thẳng $BG$ và cắt $AB$ lần lượt tại $C',D',E',F'.$

Khi đó, các điểm này chia $AB$ thành năm đoạn thẳng bằng nhau. Em hãy giải thích vì sao?

Phương pháp giải:

Dựa vào định lý Thales để chứng minh:

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Vì đường thẳng đi qua $C,D,E,F$ song song với đường thẳng $BG$ và cắt $AB$ lần lượt tại $C',D',E',F'.$ Áp dụng định lý Thales thuận ta có:

$\begin{array}{l}CC'//DD'\\ =  > \frac{{CA}}{{CD}} = \frac{{C'A}}{{C'D'}}\end{array}$

Mà $\begin{array}{l}CA = CD\\ =  > C'A = C'D'\end{array}$

Chứng minh tương tự với $DD'//EE',EE'//FF',FF'//BG$

Ta có: $AC' = C'D' = D'E' = E'F' = F'B'$.