Giải mục 2 trang 44, 45 SGK Toán 8 - Cùng khám phá
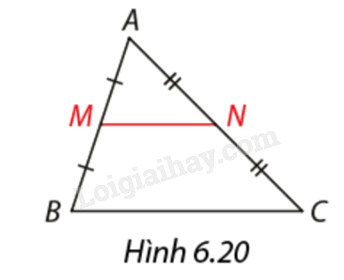
Xem hình 6.20. Giải thích vì sao đường trung bình \(MN\) song song với cạnh
Hoạt động 2
Xem hình 6.20. Giải thích vì sao đường trung bình \(MN\) song song với cạnh \(BC.\) Đo và tính tỉ số của \(MN\) và \(BC.\)
Phương pháp giải:
Sử dụng định lí Thalès đảo trong tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC.\)
Lời giải chi tiết:
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow MN//BC\) (định li Thalès đảo).
Xét tam giác \(ABC\) có \(MN//BC\) nên theo hệ quả định lí Thalès ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}.\)
Luyện tập 2
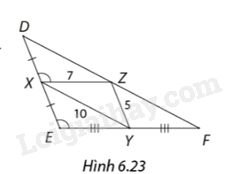
Trong Hình 6.23, giải thích vì sao \(Z\) là trung điểm của \(DF\) và tính độ dài ba cạnh tam giác \(DEF.\)
Phương pháp giải:
Dựa vào định lí Thales để giải thích vì sao Z là trung điểm của DF.
Dựa vào tính chất đường trung bình của tam giác: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết:
Xét tam giác \(DEF\) , ta có:
\(\widehat {DXZ} = \widehat {DEY}\) (mà hai góc này ở vị trí đồng vị)
=> \(XZ//EF\)
Áp dụng định lí Thales ta có:
\(\frac{{DX}}{{XE}} = \frac{{DZ}}{{ZF}} = 1\)
=> Z là trung điểm của DF
Lại có:
\(\begin{array}{l}EX = XD\\EY = YF\end{array}\)
=> X là trung điểm của DE
Y là trung điểm của EF
=> XY là đường trung bình của tam giác \(DEF\) .
Áp dụng tính chất của đường trung bình của tam giác ta có:
\(\begin{array}{l}XY = \frac{1}{2}DF\\ = > DF = 10.2 = 20\end{array}\)
Mà Z là trung điểm của DF
Y là trung điểm của EF
=> ZY là đường trung bình của tam giác DEF
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}ZY = \frac{1}{2}DE\\ = > DE = 2.5 = 10\end{array}\)
Mà X là trung điểm của DE
Z là trung điểm của DF
=> XZ là đường trung bình
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}XZ = \frac{1}{2}EF\\EF = 2.7 = 14\end{array}\)
Vậy tam giác \(DEF\) có \(DF = 20,EF = 14,DE = 10\)
Vận dụng
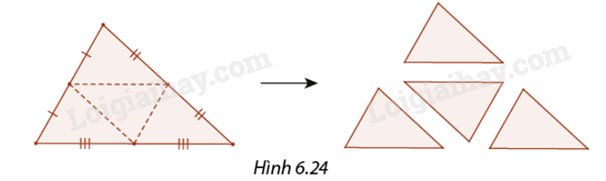
Giải thích vì sao khi cắt ba mảnh bìa hình tam giác theo ba đường trung bình của nó (Hình 6.24) thì ta được bốn tam giác bằng nhau.
Phương pháp giải:
Dựa vào tính chất đường trung bình của tam giác và các trường hợp hai tam giác bằng nhau để chứng minh.
Lời giải chi tiết:
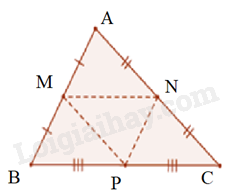
Xét tam giác \(AMN\) và \(BMP\) , ta có:
\(AM = BM\) (M là trung điểm)
\(MN = BP\) (do \(MN = BP = \frac{1}{2}BC\) )
\(MP = AN\) (do \(MP = AN = \frac{1}{2}AC\) )
=> \(\Delta AMN = \Delta BMP\left( {c - c - c} \right)\)
Chứng minh tương tự với các trường hợp còn lại. Ta được 4 tam giác bằng nhau.