Giải mục 2 trang 49, 50, 51, 52 Chuyên đề học tập Toán 10 - Kết nối tri thức
Cho điểm (M({x_0};{y_0}))thuộc hypebol có hai tiêu điểm ({F_1}( - c;0),{F_2}(c;0)), độ dài trục thực bằng 2a.
HĐ2
Cho điểm \(M({x_0};{y_0})\)thuộc hypebol có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\), độ dài trục thực bằng 2a.
a) Tính \(M{F_1}^2 - M{F_2}^2\)
b) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\), tức là,\(M{F_1} - M{F_2} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
c) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\), tức là,\(M{F_2} - M{F_1} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {M{F_1}} ( - c - {x_0}; - {y_0});\overrightarrow {M{F_2}} (c - {x_0}; - {y_0})\)
\( \Rightarrow M{F_1}^2 = {( - c - {x_0})^2} + {( - {y_0})^2};M{F_2}^2 = {(c - {x_0})^2} + {( - {y_0})^2}\)
\( \Rightarrow M{F_1}^2 - M{F_2}^2 = {( - c - {x_0})^2} - {(c - {x_0})^2} = 4c{x_0}\)
b) Khi điểm M \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) (\(M{F_1} - M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\frac{{2c}}{a}{x_0} + 2a}}{2} = a + \frac{c}{a}{x_0}\\M{F_2} = \frac{{\frac{{2c}}{a}{x_0} - 2a}}{2} = - a + \frac{c}{a}{x_0}\end{array}\)
c) Khi điểm \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) (\(M{F_2} - M{F_1} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = - \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) - 2a}}{2} = - a - \frac{c}{a}{x_0}\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) + 2a}}{2} = a - \frac{c}{a}{x_0}\end{array}\)
Câu hỏi
Hiệu độ dài hai bán kính qua tiêu của một điểm thuộc hypebol có mối quan hệ gì với độ dài trục thực?
Lời giải chi tiết:
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) thì \(M{F_1} - M{F_2} = 2a\)
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) thì \(M{F_2} - M{F_1} = 2a\)
\( \Rightarrow \left| {M{F_1} - M{F_2}} \right| = 2a\)
Luyện tập 2
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng \(6\sqrt 3 \). Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Phương pháp giải:
Độ dài trục thực bằng \(2a\), độ dài trục ảo bằng \(2b\).
Với \(M({x_0};{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {a + \frac{c}{a}{x_0}} \right|;M{F_2} = \left| {a - \frac{c}{a}{x_0}} \right|\)
Lời giải chi tiết:
Độ dài trục thực bằng \(2a = 6 \Rightarrow a = 3.\)
Độ dài trục ảo bằng \(2b = 6\sqrt 3 \Rightarrow b = 3\sqrt 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = 6\).
Với \(M(9;{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {3 + \frac{6}{3}.9} \right| = 21;M{F_2} = \left| {3 - \frac{6}{3}.9} \right| = 15.\)
Luyện tập 3
Cho hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\). Điểm M nào thuộc hypebol mà có độ dài bán kính qua tiêu \(M{F_2}\) nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm
Phương pháp giải:
\(M{F_2}\) nhỏ nhất bằng \(c - a\) khi M trùng đỉnh \({A_2}(a;0)\)
Lời giải chi tiết:
Xét hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\), ta có:
\(a = 1,b = \sqrt 3 ,c = 2\).
\( \Rightarrow M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(1;0)\)
Khi đó, \(M{F_1} = \left| {1 + \frac{2}{1}.1} \right| = 3.\)
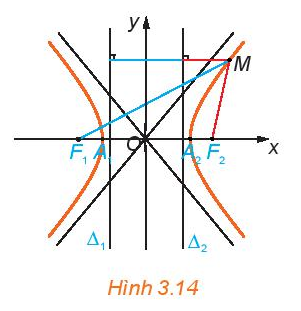
HĐ3
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} - {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = - \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).
Với điểm M (x; y) thuộc hypebol, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.
Phương pháp giải:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
Ta có:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;\;\;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
\(d(M,{\Delta _1}) = \left| {x - \left( { - \frac{{{a^2}}}{c}} \right)} \right| = \left| {x + \frac{{{a^2}}}{c}} \right|\); \(d(M,{\Delta _2}) = \left| {x - \frac{{{a^2}}}{c}} \right|\)
\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \left| {\frac{{{a^2} + cx}}{a}} \right|:\left| {\frac{{{a^2} + cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\) ;
\(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \left| {\frac{{{a^2} - cx}}{a}} \right|:\left| {\frac{{{a^2} - cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)
Luyện tập 4
Trong mặt phẳng tọa độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai \(e = 2\) và một đường chuẩn là \(x = 8\). Lập phương trình chính tắc của (H).
Phương pháp giải:
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} + {b^2}} \)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).
Lời giải chi tiết:
Phương trình chính tắc của hypebol có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
Vì \(a,c > 0\) nên \(e > 0\)
+ Đường chuẩn: \({\Delta _2}:x = 8 = \frac{a}{2} \Rightarrow a = 16\)
+ Tâm sai của hypebol: \(e = 2 \Rightarrow \frac{c}{{16}} = 2 \Rightarrow c = 32 \Rightarrow b = 16\sqrt 3 \)
Phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{256}} - \frac{{{y^2}}}{{768}} = 1\).
Vận dụng
Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt trời là \({3.10^8}\) km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15). Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^8}\) km trên thực tế.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_2}(c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc hypebol, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(a;0)\)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
Lời giải chi tiết:
\({3.10^8}\) km = 3 đơn vị.
Gọi PTCT của quỹ đạo hình hypebol đó là: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\),
Giả sử Mặt trời là tiêu điểm \({F_2}( - c;0)\).
Điểm M bất kì thuộc hypebol là vị trí của sao chổi trong quỹ đạo, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 3\) khi M trùng đỉnh \({A_2}(a;0)\)
Tâm sai của hypebol là: \(e = \frac{c}{a} = 3,6 \Rightarrow c = 3,6a\)
\( \Rightarrow 2,6a = 3 \Leftrightarrow a = \frac{{15}}{{13}},\;c = \frac{{54}}{{13}} \Rightarrow {b^2} = \frac{{207}}{{13}}\)
\( \Rightarrow \)PTCT của hypebol là: \(\frac{{169{x^2}}}{{225}} - \frac{{13{y^2}}}{{207}} = 1\),