Giải mục 2 trang 55, 56 Chuyên đề học tập Toán 10 - Kết nối tri thức — Không quảng cáo

HĐ2

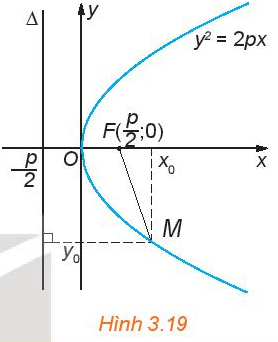
Cho parabol có phương trình chính tắc ${y^2} = 2px$ (H.3.19).

a) Nêu tọa độ điểm F và phương trình đường chuẩn của $\Delta$ của parabol.

b) Cho điểm $M({x_0};{y_0})$ thuộc parabol. Hãy so sánh MF với $d(M,\Delta )$, từ đó, tính MF theo ${x_0},{y_0}$.

Lời giải chi tiết:

a) Tiêu điểm $F(\frac{p}{2};0)$

Phương trình đường chuẩn: $\Delta :x =  - \frac{p}{2}$

b) Ta có:

$MF = \sqrt {{{\left( {{x_0} - \frac{p}{2}} \right)}^2} + {y_0}^2}  = \sqrt {{{\left( {{x_0} - \frac{p}{2}} \right)}^2} + 2p{x_0}}  = \sqrt {{{\left( {{x_0} + \frac{p}{2}} \right)}^2}}  = {x_0} + \frac{p}{2}$;

$d(M,\Delta ) = {x_0} + \frac{p}{2}$

$\Rightarrow MF = d(M,\Delta ) = {x_0} + \frac{p}{2} = {x_0} + \frac{{{y_0}^2}}{{4{x_0}}}$

Luyện tập 2

Cho parabol có phương trình ${y^2} = 8x$. Tìm tọa độ tiêu điểm và phương trình đường chuẩn của parabol. Tính bán kính qua tiêu của một điểm M thuộc parabol biết điểm có tung độ bằng 4.

Phương pháp giải:

Cho parabol có phương trình chính tắc ${y^2} = 2px$

+) Tiêu điểm $F(\frac{p}{2};0)$

+) Với $M({x_0};{y_0})$ thuộc parabol, bán kính qua tiêu: $MF = {x_0} + \frac{p}{2}$

Lời giải chi tiết:

Parabol có phương trình chính tắc ${y^2} = 8x \Leftrightarrow p = 4$

+) Tiêu điểm $F(\frac{4}{2};0) = (2;0)$

+) $M({x_0};4)$ thuộc parabol $\Rightarrow {4^2} = 8.{x_0} \Rightarrow {x_0} = 2$

Bán kính qua tiêu: $MF = {x_0} + \frac{p}{2} = 2 + \frac{4}{2} = 4.$

Luyện tập 3

Một sao chổi chuyển động theo quỹ đạo parabol nhận tâm Mặt trời làm tiêu điểm. Khoảng cách ngắn nhất từ sao chổi đến tâm Mặt Trời là ${10^6}$ km. Lập phương trình chính tắc của quỹ đạo theo đơn vị kilomet. Hỏi khi sao chổi nằm trên vuông góc với trục đối xứng của quỹ đạo tại tâm Mặt Trời, thì khoảng cách từ sao chổi đến tâm Mặt Trời là bao nhiêu kilomet?

Phương pháp giải:

Cho parabol có phương trình chính tắc ${y^2} = 2px$

+) Tiêu điểm $F(\frac{p}{2};0)$

+) Với $M({x_0};{y_0})$ thuộc parabol, $MF = {x_0} + \frac{p}{2}$

$MF$ nhỏ nhất bằng $\frac{p}{2}$ khi M trùng O(0;0).

Lời giải chi tiết:

Gọi phương trình chính tắc của parabol là: ${y^2} = 2px$

Với $M({x_0};{y_0})$ thuộc parabol, $MF = {x_M} + \frac{p}{2}$

$MF$ nhỏ nhất bằng $\frac{p}{2} = {10^6}$ khi M trùng O(0;0) nên $p = {2.10^6}$

Tiêu điểm $F(\frac{p}{2};0) = ({10^6};0)$

Khi M trên vuông góc với trục đối xứng của quỹ đạo tại tiêu điểm thì ${x_M} = {10^6}$

$\Rightarrow MF = {x_M} + \frac{p}{2} = {10^6} + {10^6} = {2.10^6}$(km)

Vận dụng

Theo các bước sau, hãy giải quyết vấn đề đã được nêu ra ở phần mở đầu bài học.

a) Tìm chiều cao của cổng mà bác Vinh đã tham quan;

b) Tìm chiều cao và chiều rộng của mô hình thu nhỏ mà bác Vinh dự định làm;

c) Tìm phương trình chính tắc của mô hình đó, theo đơn vị mét;

d) Nếu tại tiêu điểm của mô hình, bác Vinh treo một hình sao thì ngôi sao đó ở độ cao bao nhiêu mét so với mặt đất?

Lời giải chi tiết:

a) Cổng mà bác Vinh đã tham quan có PTCT ${y^2} = 48x$

$\Rightarrow p = 24$

Cổng rộng 192 m $\Rightarrow y = \frac{{192}}{2} = 96 \Rightarrow x = \frac{{{{96}^2}}}{{48}} = 192$.

Vậy cổng cao 192 m.

b) Chiều cao và chiều rộng của mô hình thu nhỏ mà bác Vinh dự định làm là 1,92m.

c) Gọi phương trình chính tắc của mô hình đó, theo đơn vị mét là ${y^2} = 2px$

Cổng cao 1,92 m và rộng 1,92 m $\Rightarrow {x_0} = 1,92;{y_0} = \frac{{1,92}}{2} = 0,96$

$\Rightarrow 0,{96^2} = 2p.1,92 \Rightarrow p = 0,24$.

Vậy phương trình chính tắc của mô hình đó là ${y^2} = 0,48x$

d)

Khoảng cách từ ngôi sao (tiêu điểm) đến đỉnh cổng (gốc tọa độ) là $\frac{p}{2} = 0,12$(m)

Độ cao của ngôi sao so với mặt đất là: $1,92 - 0,12 = 1,8(m)$

Vậy $\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.$