Giải mục 2 trang 53, 54, 55 SGK Toán 8 – Cánh diều — Không quảng cáo

HĐ2

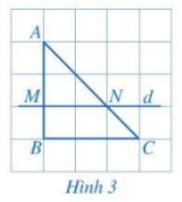
Quan sát Hình 3 và cho biết:

a)      Đường thẳng $d$ có song song với BC hay không?

b)     Bằng cách đếm số ô vuông, dự đoán xem các tỉ số $\frac{{AM}}{{MB}},\frac{{AN}}{{NC}}$ có bằng nhau hay không?

Phương pháp giải:

Quan sát hình và trả lời câu hỏi.

Lời giải chi tiết:

a)      Quan sát hình ta thấy $d\parallel BC$.

b)     Ta thấy:

Độ dài AM là 2 lần cạnh của một ô vuông.

Độ dài MB là cạnh của một ô vuông.

$\Rightarrow \frac{{AM}}{{MB}} = \frac{2}{1} = 2$

Độ dài AN là 2 lần đường chéo của một ô vuông.

Độ dài NC là độ dài đường chéo của một ô vuông.

$\Rightarrow \frac{{AN}}{{NC}} = \frac{2}{1} = 2$

Vậy $\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}$.

LT1

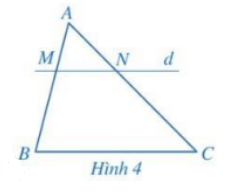
Trong Hình 4 , chứng tỏ rằng nếu $MN\parallel BC$ thì $\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}$.

Phương pháp giải:

Dựa vào định lý Thales để chứng minh hai tỉ số bằng nhau.

Lời giải chi tiết:

Xét tam giác ABC với $MN\parallel BC$, ta có $\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}$ (định lý Thales).

LT2

Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC lần lượt cắt AB, AC tại M, N. Chứng minh $\frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3}$.

Phương pháp giải:

Sử dụng định lý Thales để chứng minh $\frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3}$.

Lời giải chi tiết:

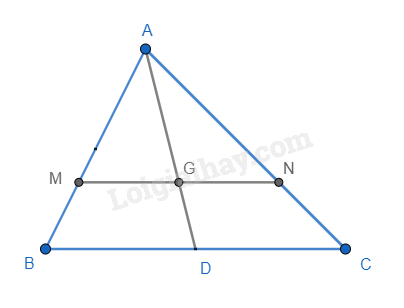
Gọi AD là đường trung tuyến của tam giác ABC (D $\in$ BC)

Vì G là trọng tâm của tam giác ABC nên AG = $\frac{2}{3}$ AD hay $\frac{AG}{AD} =\frac{2}{3}$ .

Xét tam giác ABD với MG // BD, ta có:

$\frac {AM}{AB} = \frac{AG}{AD} =\frac{2}{3}$ (Định lí Thales) (1)

Tương tự, xét

tam giác ADC với GN // DC, ta có:

$\frac {AN}{AC} = \frac{AG}{AD} =\frac{2}{3}$ (Định lí Thales) (2)

Từ (1) và (2) suy ra $\frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3}$ (đpcm).

HĐ3

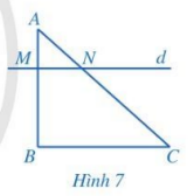
Trong Hình 7 , cho AM = 1, MB = 2, AN = 1,5, NC = 3.

a)      So sánh các tỉ số $\frac{{AM}}{{MB}};\,\,\frac{{AN}}{{NC}}$.

b)     Đường thẳng $d$ (đi qua M, N) có song song với BC hay không?

Phương pháp giải:

a)      Dựa vào số liệu đã cho, tính và so sánh các tỉ số.

b)     Quan sát hình vẽ và cho biết đường thẳng $d$ (đi qua M, N) có song song với BC hay không.

Lời giải chi tiết:

a) $\frac{{AM}}{{MB}} = \frac{1}{2}$

$\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}$

Vậy $\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}$.

b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.

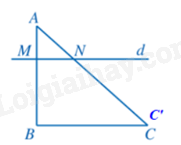
Xét ∆ABC’ với MN // BC’, ta có:

$\frac{AM}{MB}=\frac{AN}{NC′}$ (định lí Thalès).

Mà theo câu a, $\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}$ nên ta có $\frac{{AN}}{{NC}} = \frac{AN}{NC′}$

Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.

Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.

Vậy đường thẳng d (đi qua M, N) song song với BC.

LT3

Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.

Phương pháp giải:

-         Sử dụng định lý Thales đảo để chứng minh $MN\parallel AB$.

-         Chứng minh $MN \bot AC$

-         Sử dụng định lý Pytago để tính độ dài cạnh MN.

Lời giải chi tiết:

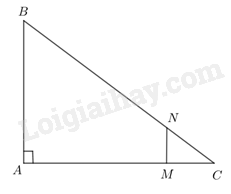
Xét tam giác ABC có

$\begin{array}{l}\frac{{CM}}{{CA}} = \frac{1}{4}\\\frac{{CN}}{{CB}} = \frac{{1,25}}{5} = \frac{1}{4}\\ \Rightarrow \frac{{CM}}{{CA}} = \frac{{CN}}{{CB}}\end{array}$

$\Rightarrow MN\parallel AB$ (Định lý Thales đảo)

Mà $AB \bot AC$ nên $MN \bot AC$ hay tam giác MNC vuông tại M

Xét tam giác MNC vuông tại M có: $MC = 1,\,\,NC = 1,25$.

Theo định lý Pytago ta có:

$\begin{array}{l}M{N^2} + M{C^2} = N{C^2}\\\,\,\,\,\,\,\,M{N^2} + {1^2} = 1,{25^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 1,{25^2} - {1^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 0,5625\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,MN = 0,75\end{array}$

Vậy MN = 0,75.