Giải mục 2 trang 63, 64 SGK Toán 8 – Cánh diều
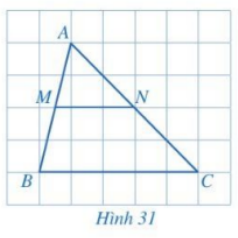
Cho tam giác ABC có MN là đường trung bình (Hình 31).
HĐ2
Cho tam giác ABC có MN là đường trung bình ( Hình 31 ).
a) MN có song song với BC hay không? Vì sao?
b) Tỉ số \(\frac{{MN}}{{BC}}\) bằng bao nhiêu?
Phương pháp giải:
a) Sử dụng định lý Thales đảo để xét khả năng song song của BC và MN.
b) Sử dụng hệ quả của định lý Thales để tính tỉ số.
Lời giải chi tiết:
a) Vì MN là đường trung bình của tam giác ABC nên M là trung điểm AB và N là trung điểm AC.
Khi đó \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) suy ra \(MN\parallel BC\) (Định lý Thales đảo trong tam giác ABC).
b) M là trung điểm AB nên \(\frac{{AM}}{{AB}} = \frac{1}{2}\).
Xét tam giác ABC với \(MN\parallel BC\) ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{2}\) (Hệ quả của định lý Thales).
LT2
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh:
a) M, N, P thẳng hàng
b) \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
Phương pháp giải:
a) Chứng minh MP và PN lần lượt là đường trung bình của hai tam giác ADC và ABC.
b) Sử dụng định lý đường trung bình của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó để chứng minh.
Lời giải chi tiết:
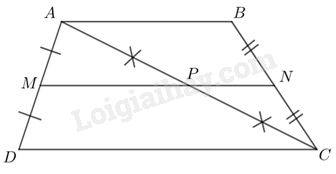
a) Vì M và P lần lượt là trung điểm của hai cạnh AD, AC nên MP là đường trung bình của tam giác ADC.
\( \Rightarrow MP\parallel AB\parallel CD\,\,\left( 1 \right)\)
Vì P và N lần lượt là trung điểm của hai cạnh AC, BC nên PN là đường trung bình của tam giác ABC.
\( \Rightarrow PN\parallel AB\parallel CD\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(MP \equiv PN\) hay ba điểm M, N, P thẳng hàng.
b) Vì MP là đường trung bình của tam giác ADC nên \(MP = \frac{1}{2}DC\).
Vì PN là đường trung bình của tam giác ABC nên \(PN = \frac{1}{2}AB\).
Ta có:
\(MN = MP + PN = \frac{1}{2}DC + \frac{1}{2}AB = \frac{1}{2}\left( {DC + AB} \right)\)
Vậy \(MN = \frac{1}{2}\left( {AB + CD} \right)\).