Giải mục 2 trang 81, 82, 83 SGK Toán 7 tập 1 - Kết nối tri thức
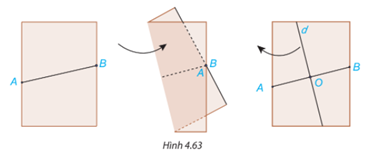
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB. Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp. a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không? b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
HĐ 3
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
Phương pháp giải:
Dùng thước đo kiểm tra.
Lời giải chi tiết:
a) O có là trung điểm của đoạn thẳng AB
b) Dùng thước đo góc ta thấy d có vuông góc với AB.
Câu hỏi
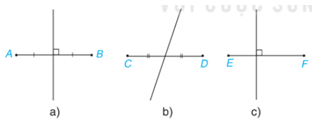
Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?
Phương pháp giải:
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Lời giải chi tiết:
Do: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Nên hình a) Lan vẽ đúng.
HĐ 4
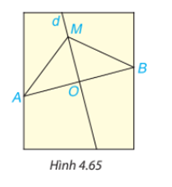
Trên mảnh giấy trong HĐ3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).
Phương pháp giải:
Dùng thước kiểm tra
Lời giải chi tiết:
Lấy điểm M bất kì trên đường thẳng d dùng thước kiểm tra ta thấy AM bằng BM.
Luyện tập 2
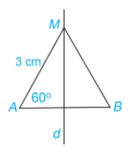
Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và \(\widehat {MAB}\)= 60° (H.4.67). Tính BM và số đo góc MBA.
Phương pháp giải:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Lời giải chi tiết:
Vì M là một điểm nằm trên đường trung trực của đoạn thẳng AB nên MA=MB=3cm.
\(\Rightarrow\) Tam giác MAB cân tại M.
\(\Rightarrow\) \(\widehat {MAB} = \widehat {MBA} = {60^o}\).