Giải mục 3 trang 65, 66 SGK Toán 8 - Cùng khám phá
Trong mỗi trường hợp ở hình 3.33, em hãy giải thích vì sao
Hoạt động 3
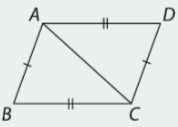
Trong mỗi trường hợp ở hình 3.33, em hãy giải thích vì sao các tam giác được cho bằng nhau và ABCD là hình bình hành.
a)
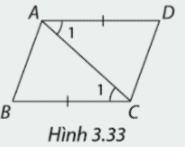
b) \(\Delta ABC = \Delta CDA.\)
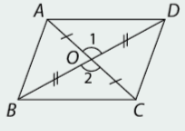
c) \(\Delta {\rm{OAD = }}\Delta {\rm{OCB}}\)
Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác suy ra hai tam giác bằng nhau.
Chứng minh các cặp cạnh đối song song và kết luận tứ giác đó là hình bình hành.
Lời giải chi tiết:
a)
Có \(AD = BC\)
AC chung \(AB = DC\)
Vậy \(\Delta ABC = \Delta CDA\left( {c - c - c} \right) \Rightarrow \widehat {ACD} = \widehat {BAC};\widehat {DAC} = \widehat {ACB}\)
Suy ra \(AD//BC;AB//DC\)
Vậy tứ giác ABCD là hình bình hành.
b)
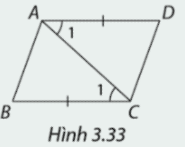
Có \(\widehat {{A_1}} = \widehat {{C_1}}\)
AC chung
\(AD = BC\)
Vậy \(\Delta ABC = \Delta CDA\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ACD} = \widehat {BAC};\widehat {DAC} = \widehat {ACB}\)
Suy ra \(AD//BC;AB//DC\)
Vậy tứ giác ABCD là hình bình hành.
c)
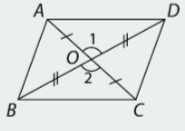
Có \(OA = OC\)
\(\widehat {{O_1}} = \widehat {{O_2}}\)(đối đỉnh)
\(OB = OD\)
Vậy \(\Delta {\rm{OAD = }}\Delta {\rm{OCB}}\) (c-g-c).
\( \Rightarrow \widehat {ACD} = \widehat {BAC};\widehat {DAC} = \widehat {ACB}\)
Suy ra \(AD//BC;AB//DC\)
Vậy tứ giác ABCD là hình bình hành.
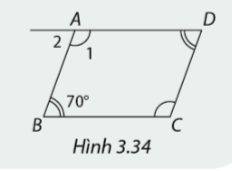
Hoạt động 4
Trong hình 3.34, tứ giác \(ABCD\) có \(\widehat {{A_1}} = \widehat C\) và \(\widehat B = \widehat D = 70^\circ .\)
Em hãy tính số đo các góc \({A_1},{A_2}\) và giải thích vì sao \(ABCD\) là hình bình hành.
Phương pháp giải:
Chứng minh tứ giác ABCD có 2 cặp cạnh song song.
Lời giải chi tiết:
Ta có \(\widehat {{A_1}} + \widehat D + \widehat C + \widehat B = 360^\circ \)
\( \Rightarrow \widehat {{A_1}} + \widehat B = 180^\circ \)\( \Rightarrow \widehat {{A_1}} = 180^\circ - \widehat B \Rightarrow \widehat {{A_1}} = 180^\circ - 70^\circ = 110^\circ .\)
Có \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {{A_2}} = 180^\circ - 110^\circ = 70^\circ .\)
Ta có \(\widehat {{A_2}} = \widehat B = 70^\circ \) mà hai góc này nằm ở vị trí so le trong nên suy ra AD//BC.
Ta có \(\widehat {{A_2}} = \widehat D = 70^\circ \) mà hai góc này nằm ở vị trí đồng vị nên suy ra AB//DC.
Vậy tứ giác ABCD là hình bình hành.
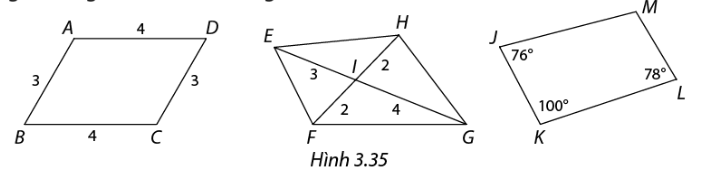
Luyện tập 2
Trong các tứ giác ở hình 3.35, tứ giác nào là hình bình hành?
Phương pháp giải:
Sử dụng dấu hiệu nhận biết của hình bình hành:
- Tứ giác có các cặp cạnh đối bằng nhau là hình bình hành.
- Tứ giác có các cặp cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có các cặp góc đối bằng nhau là hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Lời giải chi tiết:
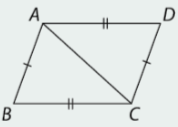
Xét tứ giác ABCD có hai cặp cạnh đối bằng nhau (\(AD = BC = 4;AB = DC = 3)\) nên ABCD là hình bình hành.
EHGF không phải hình bình hành do hai đường chéo không cắt nhau tại trung điểm mỗi đường.
JMLK không phải hình bình hành do không có hai góc đối bằng nhau.
Vận dụng
Trong Hình 3.36, Nam di chuyển thước ê ke dọc theo đường thẳng d sao cho cạnh huyền của thước luôn nằm trên d. Khi đỉnh góc \(60^\circ \) lần lượt ở vị trí điểm \(C\) và \(D.\) Nối hai điểm \(C\) và \(D,\) Nam được một đường thẳng song song với d. Em hãy giải thích vì sao?
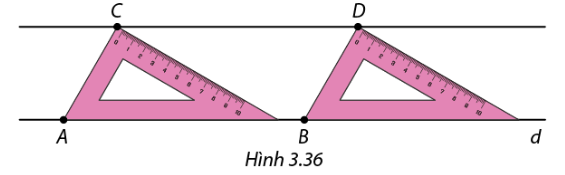
Phương pháp giải:
Ta đi chứng minh ABCD là hình bình hành và suy ra các cặp cạnh song song.
Lời giải chi tiết:
Ta thấy góc CAB bằng góc DBd mà hai góc này ở vị trí đồng vị.
Suy ra \(CA//DB\) mà \(CA = DB\) (do cùng bằng cạnh thước ê ke)
Nên suy ra \(AC{\rm{D}}B\) là hình bình hành
Suy ra \(CD//AB\) hay \(CD//d\left( {dpcm} \right)\)