Giải mục 3 trang 69, 70 SGK Toán 8 - Cùng khám phá
Cho đoạn thẳng
Hoạt động 2
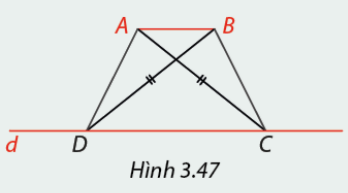
Cho đoạn thẳng \(AB\). Em hãy dựng điểm C và D trên \(d\) sao cho \(ABCD\) là hình thang có hai đường chéo \(AC = BD\) ( Hình 3.47 ). Đo các góc \(\widehat C\) và \(\widehat D\) của hình thang \(ABCD\). Nêu nhận xét và từ đó hãy cho biết tứ giác \(ABCD\) là hình gì.
Phương pháp giải:
Đo các góc \(\widehat C\) và \(\widehat D\) của hình thang \(ABCD\). Nêu nhận xét và từ đó hãy cho biết tứ giác \(ABCD\) là hình gì.
Lời giải chi tiết:
Đo hai góc \(\widehat C\) và \(\widehat D\) ta thấy hai góc này bằng nhau. Mà hai góc này cùng kề đáy CD. Vậy tứ giác \(ABCD\) là hình thang cân.
Vận dụng 2
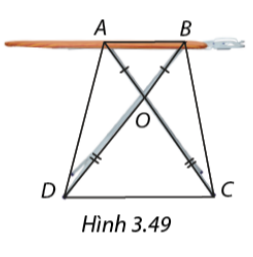
Để cầu là được thăng bằng khi là quần áo, người ta thiết kế hai chân \(AC,BD\) cắt nhau tại O sao cho \(OA = OB\) và \(OC = OD\) ( Hình 3.49 ). Giải thích vì sao khi đó đường thẳng \(AB\) trên mặt cầu là song song với đường thẳng \(CD\) trên mặt đất. Tứ giác \(ABCD\) là hình gì?
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình thang cân: Hình thang có hai hai đường chéo bằng nhau là hình thang cân.
Lời giải chi tiết:
Xét tam giác \(AOD\) và tam giác \(OBC\), ta có:
\(\begin{array}{l}OA = OB\\OD = OC\end{array}\)
\(\widehat {AOD} = \widehat {BOC}\) (2 góc này ở vị trí đối đỉnh)
→ \(\Delta AOD = \Delta BOC\)
→ \(AD = BC\)
→ \(AB//CD\)
Xét tứ giác \(ABCD\), ta có:
\(OA = OB\) và \(OC = OD\) => \(AC = BD\)
Mà hai cạnh này là hai đường chéo của tứ giác \(ABCD\)
→ Tứ giác \(ABCD\) là hình thang cân