Giải mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức
Vận dụng tọa độ của vectơ trong một số bài toán có liên quan đến thực tiễn
LT5
Trả lời câu hỏi Luyện tập 5 trang 76 SGK Toán 12 Kết nối tri thức
Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Phương pháp giải:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết:
Gọi D(x; y; z) là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm B). Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \) cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ A đến B bằng thời gian bay từ B đến D nên \(AB = BD\). Do đó, \(\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)\).
Mặt khác: \(\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)\) nên \(\left\{ \begin{array}{l}x - 940 = 140\\y - 550 = 50\\z - 8 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\;080\\y = 600\\z = 9\end{array} \right.\)
Vậy D(1 080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1 080; 600; 9).
LT1
Trả lời câu hỏi Luyện tập 6 trang 71 SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Phương pháp giải:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\)
Lời giải chi tiết:
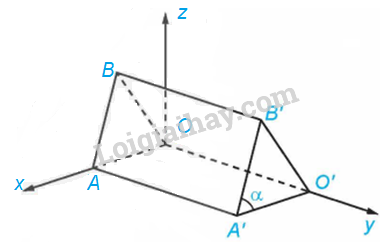
Theo Ví dụ 6 ta có: \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right);\left| {\overrightarrow {A'B'} } \right| = 60\sqrt {29} cm,O'\left( {0;450;0} \right),\)\(A'\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A'O'} = \left( { - 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A'O'} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A'B'} ;\overrightarrow {A'O'} } \right) = \frac{{\overrightarrow {A'B'} .\overrightarrow {A'O'} }}{{\left| {\overrightarrow {A'B'} } \right|.\left| {\overrightarrow {A'O'} } \right|}} = \frac{{\left( { - 120} \right)\left( { - 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B'A'O'} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)
LT7
Trả lời câu hỏi Luyện tập 7 trang 72 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
Phương pháp giải:
Sử dụng kiến thức về tính độ dài của vectơ trong không gian: Trong không gian Oxyz, cho \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải chi tiết:
Theo Ví dụ 7 ta có, khinh khí cầu thứ nhất có tọa độ là A(2; 1; 0,5), khinh khí cầu thứ hai có tọa độ là \(B\left( { - 1; - 1,5;0,8} \right)\).
Ta có: \(OA = \sqrt {{2^2} + {1^2} + 0,{5^2}} = \frac{{\sqrt {21} }}{2}km\), \(OB = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1,5} \right)}^2} + 0,{8^2}} = \frac{{\sqrt {389} }}{{10}}km\).
Vì gốc O đặt tại điểm xuất phát và \(OA > OB\) nên khinh khí cầu thứ hai gần điểm xuất phát hơn.