Giải mục 3 trang 46,47,48 SGK Toán 12 tập 2 - Kết nối tri thức
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). (H.5.29).
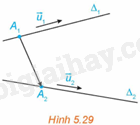
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau.
b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có cắt nhau hay không?
c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có chéo nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ trong không gian để tìm chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
Lời giải chi tiết:
a) Để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau thì giá của hai vectơ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) song song hoặc trùng nhau. Suy ra, \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
b) Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) mà \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) nên \(\overrightarrow {{A_1}{A_2}} = \overrightarrow 0 \), suy ra \({A_1}\) trùng \({A_2}\). Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
c) Vì \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) nên \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} \ne \overrightarrow 0 \) nên \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
LT8
Trả lời câu hỏi Luyện tập 8 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, chứng minh rằng hai đường thẳng sau song song với nhau:
\({\Delta _1}:\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{3}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{z}{3}\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó, \({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {3;0;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1; - 2;3} \right)\).
Đường thẳng \({\Delta _2}\) có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1; - 2;3} \right)\).
Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{3 - 1}}{1} \ne \frac{{0 - 2}}{{ - 2}} \ne \frac{1}{3}\) nên điểm \({A_1}\left( {3;0;1} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
LT9
Trả lời câu hỏi Luyện tập 9 trang 47 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 3}}{4}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y + 1}}{1} = \frac{z}{4}\). Chứng minh rằng:
a) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau;
b) Đường thẳng \({\Delta _1}\) và trục Ox chéo nhau;
c) Đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}:\frac{{x + 2}}{1} = \frac{{y + 2}}{1} = \frac{{z + 4}}{4}\);
d) Đường thẳng \({\Delta _2}\) cắt trục Oz.
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\)
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\)
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {1; - 2;3} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1;1;4} \right)\).
Đường thẳng \({\Delta _2}\) đi qua điểm \({A_2}\left( { - 1; - 1;0} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;1;4} \right)\).
a) Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{1 + 1}}{1} \ne \frac{{ - 2 + 1}}{1}\) nên điểm \({A_1}\left( {1; - 2;3} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
b) Trục Ox có một vectơ chỉ phương \(\overrightarrow i = \left( {1;0;0} \right)\) và đi qua điểm O(0;0;0).
Ta có: \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\1&0\end{array}} \right|} \right) = \left( {0;4; - 1} \right)\), \(\overrightarrow {{A_1}O} \left( { - 1;2; - 3} \right)\)
Vì \(\overrightarrow {{A_1}O} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = - 1.0 + 2.4 - 3.\left( { - 1} \right) = 11 \ne 0\) nên \({\Delta _1}\) và Ox chéo nhau.
c) Đường thẳng \({\Delta _3}\) có một vectơ chỉ phương \(\overrightarrow {{u_3}} = \left( {1;1;4} \right)\).
Vì \(\overrightarrow {{u_3}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_3}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{ - 1 + 2}}{1} = \frac{{ - 1 + 2}}{1} = \frac{{0 + 4}}{4}\) nên điểm \({A_2}\left( { - 1; - 1;0} \right)\) thuộc đường thẳng \({\Delta _3}\).
Do đó, đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}\).
d) Trục Oz có một vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\) và đi qua điểm O(0;0;0)
Ta có: \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right|} \right) = \left( {1; - 1;0} \right)\), \(\overrightarrow {{A_2}O} \left( {1;1;0} \right)\)
Vì \(\overrightarrow {{A_2}O} .\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = 1.1 - 1.1 - 0.0 = 0\) và \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {1; - 1;0} \right) \ne \overrightarrow 0 \) nên \({\Delta _2}\) cắt trục Oz.
LT10
Trả lời câu hỏi Luyện tập 10 trang 48 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, xét vị trí tương đối giữa hai đường thẳng: \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\\z = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = s\\y = 1 + 2s\\z = 3s\end{array} \right.\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để tìm vị trí tương đối của \({\Delta _1}\) và \({\Delta _2}\): Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\) và có phương trình tham số: \({\Delta _1}:\left\{ \begin{array}{l}x = {x_1} + {a_1}t\\y = {y_1} + {b_1}t\\z = {z_1} + {c_1}t\end{array} \right.\) \({\Delta _2}:\left\{ \begin{array}{l}x = {x_2} + {a_2}s\\y = {y_2} + {b_2}s\\z = {z_2} + {c_2}s\end{array} \right.\). Xét hệ phương trình hai ẩn t, s: \(\left\{ \begin{array}{l}{x_1} + {a_1}t = {x_2} + {a_2}s\\{y_1} + {b_1}t = {y_2} + {b_2}s\\{z_1} + {c_1}t = {z_2} + {c_2}s\end{array} \right.\left( * \right)\)
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và hệ (*) vô nghiệm.
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) Hệ (*) có vô số nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \)\(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương và hệ (*) vô nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \) Hệ (*) có nghiệm duy nhất
Lời giải chi tiết:
\({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\) và \(\overrightarrow {{u_2}} = \left( {1;2;3} \right)\)
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau hoặc chéo nhau.
Xét hệ phương trình: \(\left\{ \begin{array}{l}1 + 2t = s\\3 + t = 1 + 2s\\1 - t = 3s\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}s - 2t = 1\;\left( 1 \right)\\2s - t = 2\;\left( 2 \right)\\3s + t = 1\;\left( 3 \right)\end{array} \right.\)
Từ (1) và (2) ta có: \(s = 1;t = 0\), thay vào (3) ta thấy không thỏa mãn phương trình.
Do đó, hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
VD3
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Kết nối tri thức
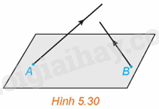
(H.5.30) Trong không gian Oxyz, có hai vật thể lần lượt xuất phát từ A(1; 2; 0) và B(3; 5; 0) với vận tốc không đổi tương ứng là \(\overrightarrow {{v_1}} = \left( {2;1;3} \right),\overrightarrow {{v_2}} = \left( {1;2;1} \right)\). Hỏi trong quá trình chuyển động, hai vật thể trên có va chạm vào nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để giải: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\).
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\).
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\).
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\) .
Lời giải chi tiết:
Gọi d là đường thẳng đi qua A và có vectơ chỉ phương là \(\overrightarrow {{v_1}} =\left( {2;1;3} \right)\).
Gọi d’ là đường thẳng đi qua B và có vectơ chỉ phương là \(\overrightarrow {{v_2}} =\left( {1;2;1} \right)\).
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên hai vectơ \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) không cùng phương.
Ta có: \(\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&3\\2&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}3&2\\1&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}2&1\\1&2\end{array}} \right|} \right) = \left( { - 5;1;3} \right) \ne \overrightarrow 0 \), \(\overrightarrow {AB} \left( {2;3;0} \right)\).
Vì \(\overrightarrow {AB} .\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( { - 5} \right).2 + 1.3 + 3.0 = - 7 \ne 0\) nên d và d’ chéo nhau.
Do đó, hai vật trên không va chạm vào nhau.