Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức
Tích vô hướng của hai vectơ trong không gian
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 54 SGK Toán 12 Kết nối tri thức
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy điểm O và vẽ các vectơ\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Lấy điểm O’ khác O và vẽ các vectơ \(\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \) (H.2.21).
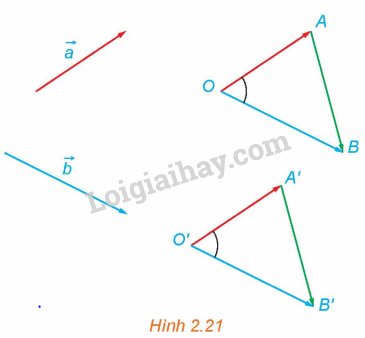
a) Hãy giải thích vì sao \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
b) Áp dụng định lí côsin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \(\widehat {AOB} = \widehat {A'O'B'}\)
Phương pháp giải:
a) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
b) Sử dụng kiến thức về định lí côsin để chứng minh: Cho tam giác ABC có, khi đó, \(\cos \widehat A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} ;\overrightarrow {A'B'} = \overrightarrow {A'O'} + \overrightarrow {O'B'} \)
Mà \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \Rightarrow \overrightarrow {AO} = \overrightarrow {A'O'} ;\overrightarrow {OB} = \overrightarrow {O'B'} \)
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \)
b) Áp dụng định lí côsin vào tam giác AOB ta có: \(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Áp dụng định lí côsin vào tam giác A’O’B’ ta có: \(\cos \widehat {A'O'B'} = \frac{{O'A{'^2} + O'B{'^2} - A'B{'^2}}}{{2.O'A'.O'B'}}\)
Vì \(\overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow AB = A'B',\overrightarrow {AO} = \overrightarrow {A'O'} \Rightarrow OA = O'A';\overrightarrow {OB} = \overrightarrow {O'B'} \Rightarrow OB = O'B'\)
Do đó, \(\cos \widehat {AOB} = \cos \widehat {A'O'B'} \Rightarrow \widehat {AOB} = \widehat {A'O'B'}\)
CH
Trả lời câu hỏi Câu hỏi trang 55 SGK Toán 12 Kết nối tri thức
Xác định góc giữa hai vectơ cùng hướng (và khác \(\overrightarrow 0 \)), góc giữa hai vectơ ngược hướng trong không gian
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Góc giữa hai vectơ cùng hướng bằng \({0^0}\).
Góc giữa hai vectơ ngược hướng bằng \({180^0}\).
LT9
Trả lời câu hỏi Luyện tập 9 trang 56 SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).
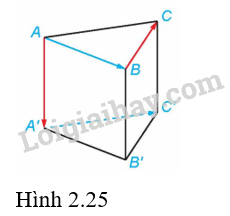
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Vì ABC.A’B’C’ là lăng trụ tam giác đều nên AA’B’B là hình chữ nhật. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \). Do đó: \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = \widehat {B'BC} = {90^0}\) (do BB’C’C là hình chữ nhật)
Vì AA’B’B là hình chữ nhật nên \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right) = \widehat {C'A'B'}\).
Vì tam giác A’B’C’ là tam giác đều nên \(\widehat {C'A'B'} = {60^0}\). Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = {60^0}\).
HD8
Trả lời câu hỏi Hoạt động 8 trang 56 SGK Toán 12 Kết nối tri thức
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau: \(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
Lời giải chi tiết:
Công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau:
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
LT10
Trả lời câu hỏi Luyện tập 10 trang 57 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 10, hãy tính các tích vô hướng \(\overrightarrow {AS} .\overrightarrow {BD} \) và \(\overrightarrow {AS} .\overrightarrow {CD} \)
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
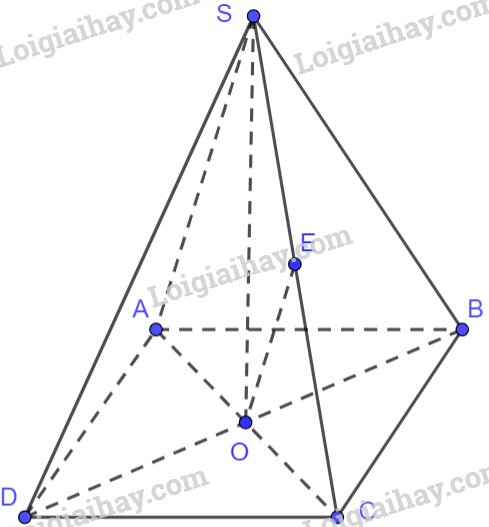
Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.
Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là \(a\sqrt 2 \)\( \Rightarrow OB = \frac{{a\sqrt 2 }}{2}\)
Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, \(OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS} = 2\overrightarrow {OE} \)
Vì O là trung điểm của BD nên \(\overrightarrow {BD} = 2\overrightarrow {OB} \)
Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên \(\Delta \)EOB vuông tại O. Do đó, \(\overrightarrow {OE} \bot \overrightarrow {OB} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {BD} = 2\overrightarrow {OE} .\left( { - 2\overrightarrow {OB} } \right) = - 4\overrightarrow {OE} .\overrightarrow {OB} = 0\)
Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {CD} = \overrightarrow {AS} .\overrightarrow {BA} = - \overrightarrow {AS} .\overrightarrow {AB} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB}\)
Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra \(\widehat {SAB} = {60^0}\)
Suy ra: \(\overrightarrow {AS} .\overrightarrow {CD} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB} = - a.a.\cos {60^0} = \frac{{ - {a^2}}}{2}\)
LT11
Trả lời câu hỏi Luyện tập 11 trang 57 SGK Toán 12 Kết nối tri thức
Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 0\).
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
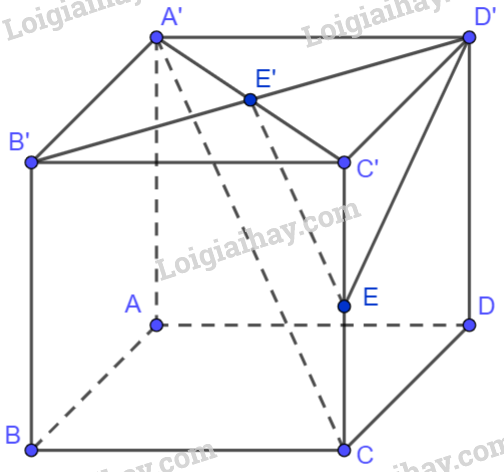
Giả sử cạnh của hình lập phương ABCD.A’B’C’D’ bằng 1. Khi đó, \(A'C' = B'D' = \sqrt 2 \)
Gọi E’ là giao điểm của hai đường chéo A’C’ và B’D’ của hình vuông A’B’C’D’. Khi đó, E’ là trung điểm của A’C’ và B’D’. Suy ra \(\overrightarrow {B'D'} = 2\overrightarrow {E'D'} \) và \(E'D' = \frac{{\sqrt 2 }}{2}\).
Gọi E là trung điểm của CC’. Mà E’ là trung điểm của A’C’ nên EE’ là đường trung bình của tam giác A’C’C. Do đó, \(\overrightarrow {A'C} = 2\overrightarrow {E'E} \) và \(E'E = \frac{1}{2}A'C\)
Áp dụng định lí Pythagore vào \(\Delta \)A’C’C vuông tại C’ có: \(A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {2 + 1} = \sqrt 3 \)\( \Rightarrow E'E = \frac{{\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào \(\Delta \)D’C’E vuông tại C’ có:
\(ED{'^2} = C'D{'^2} + C'{E^2} = 1 + \frac{1}{4} = \frac{5}{4}\)
Vì \(E'D{'^2} + E'{E^2} = \frac{1}{2} + \frac{3}{4} = \frac{5}{4} = ED{'^2}\) nên \(\Delta \)E’D’E vuông tại E’. Do đó, \(\overrightarrow {E'E} \bot \overrightarrow {E'D'} \)
Ta có: \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 2.\overrightarrow {E'E} .2.\overrightarrow {E'D'} \)\( = 0\) (đpcm)
VD4
Trả lời câu hỏi Vận dụng 4 trang 57 SGK Toán 12 Kết nối tri thức
Như đã biết, nếu có một lực \(\overrightarrow F \) tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức \(A = \overrightarrow F .\overrightarrow {MN} \), trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\overrightarrow F \) có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?

Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để giải thích: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hương của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Ta có: \(A = \overrightarrow F .\overrightarrow {MN} = \left| {\overrightarrow F } \right|.\left| {\overrightarrow {MN} } \right|.\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\)
Vì lực \(\overrightarrow F \) có độ lớn không đổi và vật di chuyển một quãng đường không đổi nên A lớn nhất khi \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\) lớn nhất. Do đó, \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = 1 \Leftrightarrow \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = {0^0}\) . Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.