Giải mục 3 trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
Khám phá 3
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
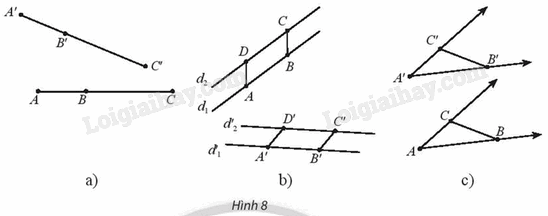
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?
b) Cho hai đường thẳng song song d 1 và d 2 , lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d 1 và d 2 . Gọi \({d_1}',{d_2}'\) lần lượt là ảnh của d 1 , d 2 và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng \({d_1}',{d_2}'\).
c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).
So sánh và \(\Delta ABC\). So sánh số đo hai góc \(\widehat {BAC}\) và \(\widehat {B'A'C'}\).
Phương pháp giải:
Quan sát hình 8 để trả lời
Lời giải chi tiết:
Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.
a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.
Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).
Suy ra AB + BC = AC.
Khi đó A’B’ + B’C’ = A’C’.
Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).
b) Ta có AB = DC (giả thiết) và AB // DC (do d 1 // d 2 ).
Suy ra tứ giác ABCD là hình bình hành.
Khi đó AD = BC.
Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.
Suy ra A’B’ = AB; D’C’ = DC.
Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)
Chứng minh tương tự, ta được A’D’ = B’C’ (2)
Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.
Khi đó A’B’ // D’C’ hay \({d_1}'{\rm{//}}{d_2}'\).
Vậy tứ giác A’B’C’D’ là hình bình hành và \({d_1}'{\rm{//}}{d_2}'\).
c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.
Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.
Do đó ∆A’B’C’ = ∆ABC (c.c.c).
Từ đó suy ra \(\widehat {B'A'C'} = \widehat {BAC}\) (cặp cạnh tương ứng).
Vậy \(\Delta A'B'C'{\rm{ }} = {\rm{ }}\Delta ABC\) và \(\widehat {B'A'C'} = \widehat {BAC}\).
Thực hành 3
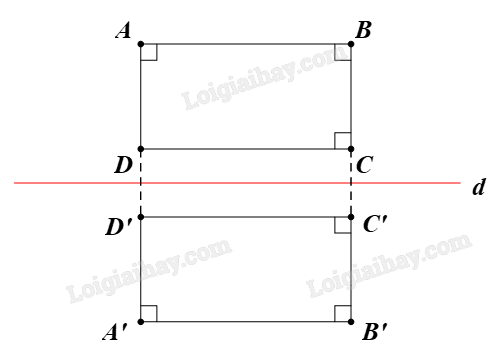
Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng . Hãy cho biết A’B’C’D’ là hình gì. Giải thích.
Phương pháp giải:
Phép dời hình bảo toàn:
- Tính thẳng hàng của 3 điểm và thứ tự của ba điểm thẳng hàng.
- Tính song song của hai đường thẳng.
- Độ lớn của một góc.
Lời giải chi tiết:
Gọi f là phép biến hình trong Vận dụng .
Trong Vận dụng , ta đã chứng minh được f là một phép dời hình.
Ta có ABCD là hình chữ nhật.
Suy ra \(\;\widehat {DAB} = 90^\circ ;\,\,\widehat {ABC} = 90^\circ ;\,\,\widehat {BCD} = 90^\circ \)
Do phép dời hình f bảo toàn độ lớn của góc nên ta có \(\widehat {{\rm{D'A'B'}}} = 90^\circ ;\widehat {{\rm{A'B'C'}}} = 90^\circ ;\widehat {{\rm{B'C'D'}}} = 90^\circ \)
Vậy A’B’C’D’ cũng là hình chữ nhật.