Giải mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
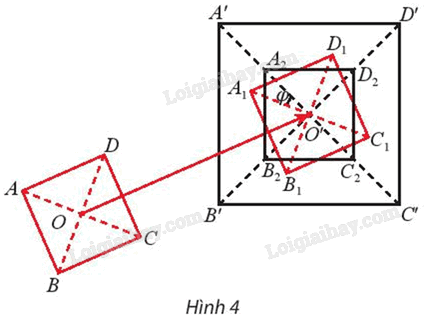
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
Thực hành 2
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi A1B1C1Đ1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A 1 , O’A’). Tìm ảnh A2B2C2Đ2 của hình vuông A 1 B 1 C 1 D 1 qua phép quay Q(O′,φ).
b) Cho biết →OA′=k→OA2. Tìm ảnh của hình vuông A2B2C2Đ2 qua phép vị tự V(O′,k).
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Phương pháp giải:
Để tìm ảnh của một hình qua một phép biến hình ta tìm ảnh của các điểm thuộc hình đó qua phép biến hình. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
a) Do phép quay là phép dời hình nên ảnh A 2 B 2 C 2 D 2 của hình vuông A 1 B 1 C 1 D 1 cũng là hình vuông có kích thước bằng hình vuông A 1 B 1 C 1 D 1 .
Theo đề, ta có A 1 B 1 C 1 D 1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo →OO′.
Mà O là tâm của hình vuông ABCD.
Nên ta có O’ là tâm của hình vuông A 1 B 1 C 1 D 1 .
Mà A 2 B 2 C 2 D 2 là ảnh của hình vuông A 1 B 1 C 1 D 1 qua Q(O′,φ) (giả thiết).
Suy ra O’ cũng là tâm của hình vuông A 2 B 2 C 2 D 2 .
Do đó O’A 2 = O’B 2 = O’C 2 = O’D 2 .
Để tìm ảnh A 2 B 2 C 2 D 2 của hình vuông A 1 B 1 C 1 D 1 qua ta tìm vị trí các điểm A 2 , B 2 , C 2 , D 2 theo thứ tự là ảnh của các điểm A 1 , B 1 , C 1 , D 1 qua Q(O′,φ).
Ta có A2=Q(O′,φ)(A1).
Suy ra O′A2=O′A1,(O′A1,O′A2)=φ.
Mà φ=(O′A1,O′A′) (giả thiết).
Do đó A 2 nằm trên đường thẳng O’A’.
Vì vậy A 2 là một điểm nằm trên đường thẳng O’A’ thỏa mãn O’A 2 = O’A 1 .
Ta có B2=Q(O′,φ)(B1).
Suy ra O′B2=O′B1,(O′B1,O′B2)=φ.
Ta có O’ là tâm của hình vuông A 2 B 2 C 2 D 2 và hình vuông A’B’C’D’.
Khi đó ^A1O′B=90o−^A2O′A1 và ^A1O′B′=90o−^A′O′A1
Suy ra ^A1O′B2=^A1O′B′
Do đó B 2 nằm trên đường thẳng O’B’.
Vì vậy B 2 là một điểm nằm trên đường thẳng O’B’ thỏa mãn O′B2=O′B1.
Chứng minh tương tự, ta được:
⦁ C 2 nằm trên đường thẳng O’C’ thỏa mãn O’C 2 = O’C 1 ;
⦁ D 2 nằm trên đường thẳng O’D’ thỏa mãn O’D 2 = O’D 1 .
Vậy ảnh của hình vuông A 1 B 1 C 1 D 1 qua Q (O’, φ) là hình vuông A 2 B 2 C 2 D 2 thỏa mãn A 2 , B 2 , C 2 , D 2 lần lượt nằm trên O’A’, O’B’, O’C’, O’D’ và O’B 2 = O’C 2 = O’D 2 = O’A 2 = O’A 1 .
b) Để tìm ảnh của hình vuông A 2 B 2 C 2 D 2 qua V (O’, k) , ta tìm ảnh của các điểm A 2 , B 2 , C 2 , D 2 qua V (O’, k) .
Theo đề, ta có →O′A′=k→O′A2 .
Suy ra V(O′,k)(A2)=A′,O′A′=|k|.O′A2.
Ta có O’A 2 = O’B 2 (chứng minh trên) và O’A’ = O’B’ (O’ là tâm của hình vuông A’B’C’D’).
Suy ra O′B2O′B′=O′A2O′A′=1|k|
Do đó O’B’ = |k|.O’B 2 .
Mà →O′B′,→O′B2 cùng phương (B 2 là một điểm nằm trên đường thẳng O’B’).
Suy ra →O′B′=k.→O′B2
Do đó V(O′,k)(B2)=B′.
Chứng minh tương tự, ta được V(O′,k)(C2)=C′,V(O′,k)(Đ2)=D′.
Vậy ảnh của hình vuông A 2 B 2 C 2 D 2 qua V(O′,k) là hình vuông A’B’C’D’.
c) Từ kết quả của câu a) và b), ta thấy phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O’, góc quay φ = (O’A 1 , O’A’) và phép vị tự tâm O, tỉ số k biến hình vuông ABCD thành hình vuông A’B’C’D’.
Do đó hai hình vuông ABCD và A’B’C’D’ đồng dạng với nhau.
Vậy hai hình vuông tùy ý luôn đồng dạng với nhau.
Vận dụng 2
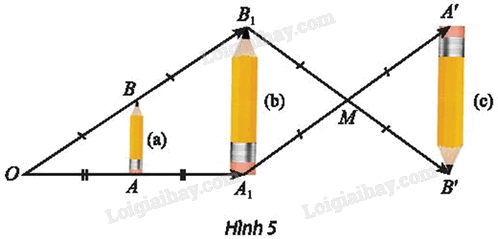
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Phương pháp giải:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải chi tiết:
⦁ Xét cặp hình (a) và (b):
Ta có OA1=2OA và →OA1,→OA cùng phương.
Suy ra →OA1=2→OA
Do đó V(O,2)(A)=A1.
Chứng minh tương tự, ta được V(O,2)(B)=B1.
Vì vậy V(O,2)(AB)=A1B1.
Khi đó V(O,2) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B 1 B’.
Suy ra B′=ĐM(B1).
Chứng minh tương tự, ta được A′=ĐM(A1).
Do đó
Khi đó ĐM biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp V(O,2) và ĐM biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).