Giải mục 4 trang 62 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
Hoạt động 6
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
a) Tìm hình chiếu \(d\) của \(A'C\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C\) và \(d\)
b) Tìm hình chiếu \(a\) của \(A'C'\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C'\) và \(a\)
Phương pháp giải:
a) Chứng minh \(A'A \bot \left( {ABCD} \right)\) từ đó suy ra \(A'\) là hình chiếu của \(A\) trên \(\left( {ABCD} \right)\)
b) Chứng minh \(CC' \bot \left( {ABCD} \right)\) từ đó suy ra \(C'\) là hình chiếu của \(C\) trên \(\left( {ABCD} \right)\)
Lời giải chi tiết:
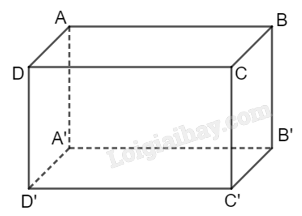
a) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(d\) của \(A'C\) trên \(\left( {ABCD} \right)\) là \(AC\)
Góc giữa \(A'C\) và \(AC\) là góc \(\widehat {A'CA}\)
b) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vì \(CC' \bot \left( {ABCD} \right)\) nên \(C\) là hình chiếu của \(C'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(a\) của \(A'C'\) trên \(\left( {ABCD} \right)\) là \(AC\)
Vì \(A'C'//AC\) nên góc giữa \(A'C'\) và \(AC\) bằng \({0^o}\)
Luyện tập 8
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Xác định và tính góc giữa đường thẳng \(SD\) và \(\left( {SAB} \right)\)
Phương pháp giải:
Xác định giao điểm \(S\) của \(SD\) và \(\left( {SAB} \right)\)
Chứng minh \(DA \bot \left( {SAB} \right)\) từ đó suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\) suy ra góc cần tìm là góc giữa 2 đường thẳng \(SD\) và \(SA\)
Sử dụng tỉ số lượng giác trong tam giác vuông
Lời giải chi tiết:
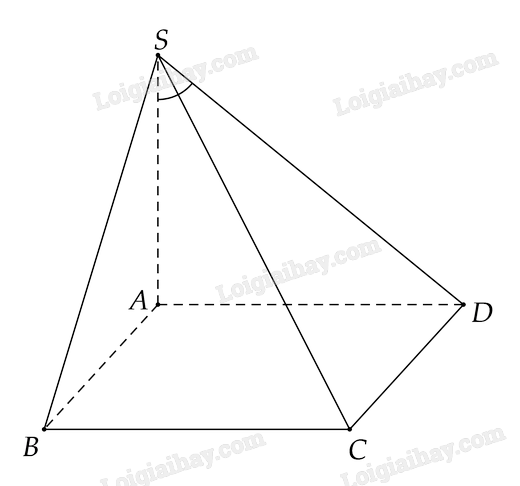
Ta có \(S\) là giao điểm của \(SD\) và \(\left( {SAB} \right)\) \(\left( 1 \right)\)
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Vì \(ABCD\) là hình vuông lên \(AD \bot AB\)
Ta có \(\left\{ \begin{array}{l}AD \bot SA\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow \)\(A\) là hình chiếu vuông góc của \(D\) trên \(\left( {SAB} \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\)
Vậy góc giữa \(SD\) và \(\left( {SAB} \right)\) là góc giữa \(SA\) và \(SD\) là góc giữa \(\widehat {DSA}\)
Xét \(\Delta SAD\) vuông tại \(A\) có \(\tan S = \frac{{AD}}{{SA}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {ASD} = {30^o}\)