Giải mục 3 trang 110, 111 SGK Toán 11 tập 1 - Cùng khám phá
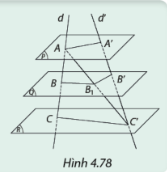
Cho ba mặt phẳng dôi một song song (P), (Q), (R) cắt hai đường thẳng d, d' lần lượt tại A, B, C và A', B', C'. Gọi B1, là giao điểm của đường thẳng AC' và mặt phẳng (Q). Tìm mối liên hệ giữa các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C}}\); \(\frac{{A'}{B'}}{{B'}{C'}}\) và \(\frac{{A{B_1}}}{{{B_1}C}}\); \(\frac{{AB}}{{BC}}\) và \(\frac{{A'}{B'}}{{B'}{C'}}\).
Hoạt động 5
Cho ba mặt phẳng dôi một song song (P), (Q), (R) cắt hai đường thẳng d, d' lần lượt tại A, B, C và A', B', C'. Gọi B 1 , là giao điểm của đường thẳng AC' và mặt phẳng (Q). Tìm mối liên hệ giữa các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C}}\); \(\frac{{A'}{B'}}{{B'}{C'}}\) và \(\frac{{A{B_1}}}{{{B_1}C}}\); \(\frac{{AB}}{{BC}}\) và \(\frac{{A'}{B'}}{{B'}{C'}}\).
Phương pháp giải:
- Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
- Áp dụng định lý Thalès trong tam giác.
Lời giải chi tiết:
(ACC') lần lượt cắt (Q) và (R) theo hai giao tuyến BB 1 và CC'. Do đó, BB 1 // CC'.
(AA'C') lần lượt cắt (P) và (Q) theo hai giao tuyến AA' và B'B 1 . Do đó, AA' // B'B 1 .
Xét tam giác ACC' có BB 1 // CC', suy ra: \(\frac{{AB}}{{BC}} = \frac{{A{B_1}}}{{{B_1}C}}\) (Định lý Thalès)
Xét tam giác AA'C' có AA' // B'B 1 , suy ra: \(\frac{{A'}{B'}}{{B'}{C'}} = \frac{{A{B_1}}}{{{B_1}C}}\) (Định lý Thalès)
\( \Rightarrow \frac{{AB}}{{BC}} = \frac{{A'}{B'}}{{B'}{C'}}\left( { = \frac{{A{B_1}}}{{{B_1}C}}} \right)\).
Luyện tập 6
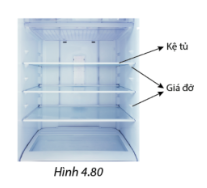
Các kệ trong ngăn mát của tủ lạnh có thể xem là hình ảnh của các mặt phẳng (Hình 4.80). Thông tin từ nhà sản xuất là các kệ này được lắp song song với nhau. Bề mặt bên trái và bên phải của tủ lạnh có các giá đỡ bên dưới các kệ. Nếu các giá đỡ ở mặt bên trái cách đều nhau một khoảng 15 cm thì các giá đỡ ở mặt bên phải cách nhau bao nhiêu? Vì sao?
Phương pháp giải:
Áp dụng định lý Thalès cho 3 mặt phẳng.
Lời giải chi tiết:
Ba ngăn mát là 3 mặt phẳng song song chắn 2 cạnh tủ thành các đoạn thẳng tương ứng tỉ lệ. Mà giá đỡ ở mặt bên trái cách đều nhau một khoảng 15 cm cho nên các giá đỡ ở mặt bên phải cũng cách nhau 15 cm vì