Giải mục 3 trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1 - Cùng khám phá
Cho hàm số \(y = f(x) = \frac{1}{x}\)
Hoạt động 6
Cho hàm số \(y = f(x) = \frac{1}{x}\)
a, Tìm tập xác định của hàm số.
b, Tính giá trị của hàm số tại các điểm trong bảng giá trị sau:

c, Nhận xét gì về giá trị của f(x) khi x dần đến \( + \infty \)? Khi x dần đến \( - \infty \)?
Phương pháp giải:
Tập xác định là các giá trị của x để hàm số có nghĩa.
Thay giá trị của x vào hàm số để được các giá trị của f(x) tương ứng.
Lời giải chi tiết:
a, Tập xác định: R\{0}.
b, Thay lần lượt các giá trị của x vào f(x) ta được:
\(\)x dần đến \( - \infty \) thì f(x)=0
\(f( - {10^8}) = \frac{1}{{ - {{10}^8}}} = - {10^{ - 8}}\)
\(f(10) = \frac{1}{{10}}\)
\(f( - {10^3}) = \frac{1}{{ - {{10}^3}}} = - {10^{ - 3}}\)
\(f(1000) = \frac{1}{{1000}} = {10^{ - 3}}\)
\(f( - {10^2}) = \frac{1}{{ - {{10}^2}}} = - {10^{ - 2}}\)
\(f(100000) = \frac{1}{{100000}} = {10^{ - 5}}\)
\(f( - 10) = \frac{1}{{ - 10}} = \frac{{ - 1}}{{10}}\)
\(f({10^9}) = \frac{1}{{{{10}^9}}} = {10^{ - 9}}\)
x dần đến \( + \infty \) thì f(x)=0.

c, Khi x dần đến và x dần đến thì f(x)=0.
Luyện tập 7
Cho hàm số \(f(x) = \frac{{\sqrt {{x^2} + 1} }}{x}\). Tìm \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x)\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Với x dần đến \( + \infty \) thì |x| = x.
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} < 0\) và \(\lim {x_n} = - \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{ - {x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim ( - \sqrt {1 + \frac{1}{{x_n^2}}} ) = - 1\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} > 0\) và \(\lim {x_n} = + \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{{x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \sqrt {1 + \frac{1}{{x_n^2}}} = 1\)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\).
Luyện tập 8
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}}\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ; - 5) \cup ( - 5; + \infty )\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\left| x \right|.\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 - \frac{4}{{{x^2}}}} = - 1\) , lim 1=1 và \(\mathop {\lim }\limits_{x \to - \infty } \frac{5}{x} = 0\) ta có:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}} = - 1\).
Hoạt động 7
Cho hàm số \(f(x) = {x^2}\) và dãy số \(({x_n})\) với \({x_n} = n + 1\)
a, Tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Tính \(f({x_n})\) theo n và tìm \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Phương pháp giải:
a, Thay \({x_n} = n + 1\) để tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) để tìm \(f({x_n})\)
Dựa vào câu a để xác định \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Lời giải chi tiết:
a, Ta có: \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = \lim (n + 1)\)
\(\mathop {\lim }\limits_{n \to - \infty } (n + 1) = - \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } (n + 1) = + \infty \).
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) ta được:
\(f({x_n}) = {(n + 1)^2}\)
\(\mathop {\lim }\limits_{n \to - \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to - \infty } {(n + 1)^2} = + \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to + \infty } {(n + 1)^2} = + \infty \).
Luyện tập 9
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x}\)
Phương pháp giải:
Chia tử cho mẫu để tính giới hạn
Lời giải chi tiết:
Hàm số \(f(x) = \frac{{{x^2} + 1}}{x} = x + \frac{1}{x}\) có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
\(\forall ({x_n}),{x_n} < 0\)và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \), ta có \(\lim f({x_n}) = \lim ({x_n} + \frac{1}{{{x_n}}}) = {\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}})\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im x}}_n^2 = + \infty \) nên \(\lim \frac{1}{{x_n^2}} = 0\). Suy ra \(\lim (1 + \frac{1}{{x_n^2}}) = 1\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \) và \(\lim (1 + \frac{1}{{x_n^2}}) = 1\) nên \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}}) = - \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x} = - \infty \).
Hoạt động 8
Cho hàm số \(f(x) = \frac{{x - 1}}{{x + 1}}\) và g(x)=x+1
a, Tìm \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } g(x)\)
b, Tìm \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\).
Phương pháp giải:
a, Với f(x) chia tử cho mẫu để tìm giới hạn
Với g(x) thì \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Tính f(x). g(x) và dựa vào câu a xác định \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\)
Lời giải chi tiết:
a, Hàm số \(f(x) = \frac{{x - 1}}{{x + 1}} = 1 - \frac{2}{{x + 1}}\) có tập xác định \(( - \infty , - 1) \cup ( - 1; + \infty )\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{2}{{x + 1}}) = 1\)
\(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Ta có: \(f(x).g(x) = \frac{{x - 1}}{{x + 1}}.(x + 1) = x - 1\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x).g(x) = \mathop {\lim }\limits_{x \to + \infty } (x - 1) = + \infty \).
Luyện tập 10
Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\).
Phương pháp giải:
Xác định \(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \) để tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \)=0 và \(\sqrt {{x^2} + 2x} > 0,\forall x > 0\) nên \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }} = + \infty \).
Vận dụng
Trong một cuộc thi các môn thể thao trên tuyết, người ta muốn thiết kế một đường trượt bằng bang cho nội dung đổ dốc tốc độ đường dài
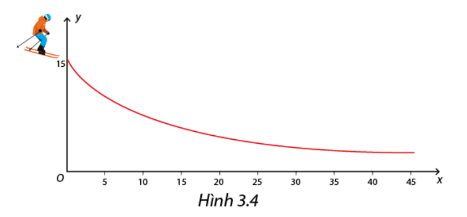
Vận động viên sẽ xuất phát từ vị trí (0; 15) cao 15 m so với mặt đất (trục 0x) . Đường trượt phải thỏa mãn yêu cầu là càng ra xa thì càng gần mặt đất để tiết kiệm lượng tuyết nhân tạo. Một nhà thiết kế đề nghị sử dụng đường cong là đồ thị \(y = f(x) = \frac{{150}}{{x + 10}}\) với \(x \ge 0\). Hãy kiểm tra xem hàm số y=f(x) có thỏa mãn các điều kiện dưới đây hay không:
a, Có đồ thị đi qua điểm (0,15)
b, Giảm trên \(\left[ {0, + \infty } \right]\)
c, Càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.
Phương pháp giải:
a, Thay tọa độ (0,15) vào hàm số để kiểm tra điểm có thuộc hàm số hay không?
b, Nhận xét với x càng tăng thì giá trị f(x) càng giảm
c, Tính lim f(x) khi x dần đến \( + \infty \)
Lời giải chi tiết:
a, Thay x=0 vào hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) ta được:
\(y = \frac{{150}}{{0 + 10}} = \frac{{150}}{{10}} = 15\)
Vậy điểm (0,15) thuộc đồ thị hàm số.
b, Nhận thấy khi x càng tăng thì giá trị hàm số càng giảm. Vậy hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) giảm trên \(\left[ {0, + \infty } \right]\)
c, Ta có : \(\mathop {\lim }\limits_{x \to + \infty } \frac{{150}}{{x + 10}} = 0\)
Vậy càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.