Giải mục 3 trang 47, 48, 49 SGK Toán 11 tập 1 - Cùng khám phá
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
Hoạt động 6
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
a) So sánh \({u_{n + 1}}\) và \({u_n}\).
b) So sánh \({v_{n + 1}}\) và \({v_n}\).
Phương pháp giải:
Thay n = n + 1 vào công thức tổng quát của dãy số. So sánh \({u_{n + 1}} - {u_n}\), \({v_{n + 1}} - {v_n}\) với 0.
Lời giải chi tiết:
a) Ta có: \({u_{n + 1}} - {u_n} = 1 + \frac{1}{{n + 1}} - 1 - \frac{1}{n} = \frac{1}{{n + 1}} - \frac{1}{n} = \frac{{n - \left( {n + 1} \right)}}{{n\left( {n + 1} \right)}} = \frac{ -1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{ -1}{{n\left( {n + 1} \right)}} < 0\)\( \Rightarrow {u_{n + 1}} - {u_n} < 0 \Rightarrow {u_{n + 1}} < {u_n}\).
b) Ta có: \({v_{n + 1}} - {v_n} = 2 - \frac{1}{{n + 1}} - 2 + \frac{1}{n} = \frac{1}{n} - \frac{1}{{n + 1}} = \frac{{n + 1 - n}}{{n\left( {n + 1} \right)}} = \frac{1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{1}{{n\left( {n + 1} \right)}} > 0 \Rightarrow {v_{n + 1}} - {v_n} > 0 \Rightarrow {v_{n + 1}} > {v_n}\).
Luyện tập 5
Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) cho bởi \({u_n} = \frac{{n - 2}}{{3n - 1}},\forall n \in {\mathbb{N}^*}\) là một dãy số tăng.
Phương pháp giải:
So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
Lời giải chi tiết:
\(\begin{array}{l}{u_{n + 1}} = \frac{{n + 1 - 2}}{{3(n + 1) - 1}} = \frac{{n - 1}}{{3n + 2}}\\{u_{n + 1}} - {u_n} = \frac{{n - 1}}{{3n + 2}} - \frac{{n - 2}}{{3n - 1}} = \frac{5}{{9{n^2} + 3n - 2}}\\9{n^2} + 3n - 2 > 0\forall n \ge 1 \Rightarrow \frac{5}{{9{n^2} + 3n - 2}} > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0\end{array}\)
\(\Rightarrow {u_{n + 1}} > {u_n}\forall n\)
Vậy dãy số đã cho là một dãy số tăng.
Hoạt động 7
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\sqrt n }}{{n + 1}}\)
a) So sánh n + 1 và \(2\sqrt n \) .
b) Suy ra: \({u_n} \le \frac{1}{2}\), với mọi số nguyên dương n.
Phương pháp giải:
a) So sánh \(n + 1 - 2\sqrt n \) với 0.
b) Áp dụng phần a.
Lời giải chi tiết:
a) \(n + 1 - 2\sqrt n = {\left( {\sqrt n - 1} \right)^2} \ge 0\forall n \Rightarrow n + 1 \ge 2\sqrt n \)
b) \(n + 1 \ge 2\sqrt n \Rightarrow \frac{{\sqrt n }}{{n + 1}} \le \frac{{\sqrt n }}{{2\sqrt n }} = \frac{1}{2} \Rightarrow {u_n} = \frac{1}{2}\forall n\) nguyên dương
Luyện tập 6
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n - 1}}{{n + 2}}\), với n là số nguyên dương.
a) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) tăng.
b) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) bị chặn.
Phương pháp giải:
a) So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
b) Dãy số \(\left( {{u_n}} \right)\) bị chặn khi \(m \le {u_n} \le M\forall n\) nguyên dương.
Lời giải chi tiết:
a)
\(\begin{array}{l}{u_n} = \frac{{n - 1}}{{n + 2}} = 1 - \frac{3}{{n + 2}}\\{u_{n + 1}} - {u_n} = 1 - \frac{3}{{n + 3}} - \left( {1 - \frac{3}{{n + 2}}} \right) = \frac{3}{{n + 2}} - \frac{3}{{n + 3}} = 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right)\\n + 2 < n + 3 \Rightarrow \frac{1}{{n + 2}} > \frac{1}{{n + 3}} \Leftrightarrow \frac{1}{{n + 2}} - \frac{1}{{n + 3}} > 0 \Leftrightarrow 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right) > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\end{array}\)
Vậy dãy số đã cho là dãy số tăng.
b) n là số nguyên dương \( \Rightarrow n \ge 1 \Leftrightarrow \left\{ \begin{array}{l}n - 1 \ge 0\\n + 2 > 0\end{array} \right. \Leftrightarrow \frac{{n - 1}}{{n + 2}} \ge 0\)
\(n - 1 < n + 2 \Rightarrow \frac{{n - 1}}{{n + 2}} < 1\)
\( \Rightarrow 0 \le \frac{{n - 1}}{{n + 2}} < 1\forall n\) nguyên dương
Vậy dãy số đã cho là dãy số bị chặn.
Vận dụng
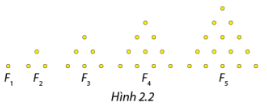
Trong một trò chơi của trẻ em, các em nhỏ dùng các viên bi để xếp thành các hình tam giác F n . Dãy các hình xếp (F n ) tuân theo một quy luật được mô tả trong Hình 2.2. Trong đó F 1 chỉ có 1 viên bi, thêm 2 viên bi để được tam giác đều là hình F 2 , thêm 3 viên bi thẳng hàng và song song với một cạnh của F 2 để được tam giác đều F 3 ,… Gọi (u n ) là dãy số mà u n là số viên bi cần dùng để xếp được hình F n \(\left( {n \in {\mathbb{N}^*}} \right)\). Chẳng hạn \({u_1} = 1,{u_2} = 3,{u_3} = 6\),…
a) Viết sáu số hạng đầu tiên của dãy số (u n ).
b) Dự đoán công thức truy hồi để tính u n .
Phương pháp giải:
Số hạng đứng sau hơn số hạng đứng trước đúng một số bằng số thứ tự của số hạng đứng sau.
Lời giải chi tiết:
a) \({u_1} = 1,{u_2} = 3,{u_3} = 6,{u_4} = 6 + 4 = 10,{u_5} = 10 + 5 = 15,{u_6} = 15 + 6 = 21\)
b) Công tính truy hồi: \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + n + 1\end{array} \right.\)