Giải mục 3 trang 26, 27, 28, 29, 30 SGK Toán 11 tập 1 - Cùng khám phá
a) Xét các số thực x1, x2, sao cho \(0 < {x_1} < {x_2} < \frac{\pi }{2}\). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x1 rad và x2 rad. Hãy so sánh tung độ của M và N, từ đó so sánh \(\sin {x_1}\) và \(\sin {x_2}\).
Hoạt động 7
a) Xét các số thực x 1, x 2 , sao cho \(0 < {x_1} < {x_2} < \frac{\pi }{2}\). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x 1 rad và x 2 rad. Hãy so sánh tung độ của M và N, từ đó so sánh \(\sin {x_1}\) và \(\sin {x_2}\).
b) Xét các số thực x 3 , x 4 , sao cho \(\frac{\pi }{2} < {x_1} < {x_2} < \pi \). Gọi P và Q lần lượt là điểm biểu diễn của góc lượng giác có số đo x 3 rad và x 4 rad. Hãy so sánh tung độ của P và Q, từ đó so sánh \(\sin {x_3}\) và \(\sin {x_4}\).
Phương pháp giải:
Lấy x 1, x 2 và x 3 , x 4 bất kì thỏa mãn yêu cầu của đề bài. Tung độ của các điểm M, N, P, Q chính là \(\sin {x_1}\), \(\sin {x_2}\), \(\sin {x_3}\), \(\sin {x_4}\). Tính \(\sin {x_1}\), \(\sin {x_2}\), \(\sin {x_3}\), \(\sin {x_4}\). Từ đó so sánh các giá trị này.
Lời giải chi tiết:
a)
\(\begin{array}{l}{x_1} = \frac{\pi }{6} \Rightarrow \sin \frac{\pi }{6} = \frac{1}{2}\\{x_2} = \frac{\pi }{3} \Rightarrow \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\ \Rightarrow \sin {x_1} < \sin {x_2}\end{array}\)
b)
\(\begin{array}{l}{x_3} = \frac{{2\pi }}{3} \Rightarrow \sin \frac{{2\pi }}{3} = \frac{{\sqrt 3 }}{2}\\{x_4} = \frac{{5\pi }}{6} \Rightarrow \sin \frac{{5\pi }}{6} = \frac{1}{2}\\ \Rightarrow \sin {x_3} > \sin {x_4}\end{array}\)
Luyện tập 7
a) Dựa vào đồ thị hàm số \(y = \sin x\), xác định tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\sin x = 0\).
b) Xác định các khoảng nghịch biến của hàm số \(y = \sin x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \sin x\).
Lời giải chi tiết:
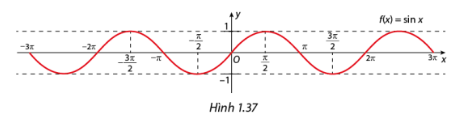
a) Dựa vào đồ thị hàm số \(y = \sin x\) trên đoạn \(x \in \left[ { - 3\pi ;3\pi } \right]\), ta có \(\sin x = 0\) khi \(x \in \left\{ { - 3\pi ; - 2\pi ; - \pi ;0;\pi ;2\pi ;3\pi } \right\}\).
b) Các khoảng nghịch biến của hàm số \(y = \sin x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\) là \(\left( { - 3\pi ; - \frac{{5\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
Hoạt động 8
Xét các số thực x 1, x 2 sao cho \(0 < {x_1} < {x_2} < \pi \). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x 1 rad và x 2 rad. Hãy so sánh hoành độ của M và N, từ đó so sánh \(\cos {x_1}\) và \(\cos {x_2}\).
Phương pháp giải:
Lấy x 1, x 2 bất kì thỏa mãn yêu cầu của đề bài. Hoành độ của các điểm M, N chính là \(\cos {x_1},\cos {x_2}\). Tính \(\cos {x_1},\cos {x_2}\). Từ đó so sánh các giá trị này.
Lấy x 1, x 2 bất kì thỏa mãn yêu cầu của đề bài. Hoành độ của các điểm M, N chính là \(\cos {x_1},\cos {x_2}\) . Tính \(\cos {x_1},\cos {x_2}\) . Từ đó so sánh các giá trị này.
Lời giải chi tiết:
\(\begin{array}{l}{x_1} = \frac{\pi }{6} \Rightarrow \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\\{x_2} = \frac{\pi }{4} \Rightarrow \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \cos {x_1} > \cos {x_2}\end{array}\)
Luyện tập 8
a) Dựa vào đồ thị hàm số \(y = \cos x\), xác định tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\cos x = - 1\).
b) Xác định các khoảng nghịch biến của hàm số \(y = \cos x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \cos x\).
Lời giải chi tiết:
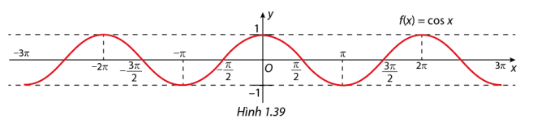
a) Dựa vào đồ thị hàm số \(y = \cos x\), tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\cos x = - 1\) là \( - 3\pi , - \pi ,\pi ,3\pi \).
b) Các khoảng nghịch biến của hàm số \(y = \cos x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\) là \(\left( { - 2\pi ; - \pi } \right),\left( {0;\pi } \right),\left( {2\pi ;3\pi } \right)\).
Vận dụng 2
Giả sử nhiệt độ bên trong một ngôi nhà sau t giờ kể từ 12 giờ trưa, gọi là \(T\left( t \right)\), được tính bởi công thức: \(T\left( t \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi t}}{6}} \right) + 25\left( {^0C} \right)\), \(0 \le t \le 24\).
a) Tìm nhiệt độ bên trong ngôi nhà lúc 12 giờ trưa, 6 giờ tối, 12 giờ đêm theo công thức trên.
b) Theo công thức trên, nhiệt độ cao nhất bên trong ngôi nhà là bao nhiêu?
Phương pháp giải:
a) t giờ được tính kể từ 12 giờ trưa nên t lúc 12 giờ trưa bằng 0, lúc 6 giờ tối bằng 6, lúc 12 giờ đêm bằng 12. Thay t = 0, 6, 12 lần lượt vào công thức.
b) Dựa vào \(\cos a \le 1\forall a\) để lập luận.
Lời giải chi tiết:
a) \(T\left( 0 \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .0}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
\(T\left( 6 \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .6}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
\(T\left( {12} \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
Vậy nhiệt độ bên trong ngôi nhà lúc 12 giờ trưa, 6 giờ tối, 12 giờ đêm đều là \({25^0}C\).
b)
\(\begin{array}{l}\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) \le 1\forall t\\ \Leftrightarrow 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) \le 5\forall t\\ \Leftrightarrow \cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) + 25 \le 30\forall t\end{array}\)
Vậy nhiệt độ cao nhất trong nhà là \({30^0}C\).
Hoạt động 9
a) Chép lại và hoàn thành bảng sau:
|
x |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
|
\(\tan x\) |
? |
? |
? |
b) So sánh \(\tan \frac{\pi }{6},\tan \frac{\pi }{4}\) và \(\tan \frac{\pi }{3}\).
Phương pháp giải:
Thay \(x = \frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3}\) vào \(\tan x\) để tính rồi so sánh.
Lời giải chi tiết:
a)
|
x |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
|
\(\tan x\) |
\(\frac{{\sqrt 3 }}{3}\) |
1 |
\(\sqrt 3 \) |
b) \(\tan \frac{\pi }{6} < \tan \frac{\pi }{4} < \tan \frac{\pi }{3}\).
Luyện tập 9
Xác định các khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \tan x\).
Lời giải chi tiết:
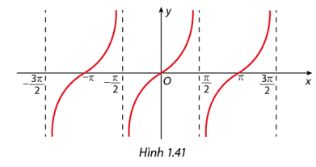
Khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\) là \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Hoạt động 10
a) Chép lại và hoàn thành bảng sau:

b) So sánh các giá trị của trong bảng trên.
Phương pháp giải:
Thay \(x = \frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3},\frac{\pi }{2},\frac{{2\pi }}{3},\frac{{3\pi }}{4},\frac{{5\pi }}{6}\) vào \(\cot x\) để tính rồi so sánh.
Lời giải chi tiết:
a)
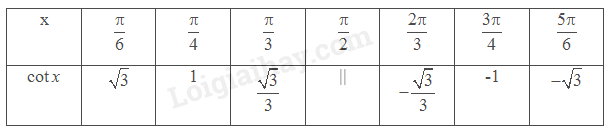
b) \(\cot \frac{\pi }{6} > \cot \frac{\pi }{4} > \cot \frac{\pi }{3} > \cot \frac{{2\pi }}{3} > \cot \frac{{3\pi }}{4} > \cot \frac{{5\pi }}{6}\)
Luyện tập 10
Xác định các khoảng nghịch biến của hàm số \(y = \cot x\) trên \(\left( { - 2\pi ;2\pi } \right)\backslash \left\{ { - \pi ;0;\pi } \right\}\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \cot x\).
Lời giải chi tiết:
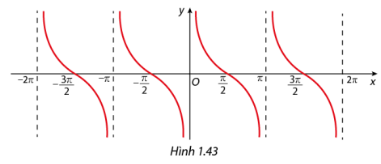
Các khoảng nghịch biến của hàm số \(y = \cot x\) trên \(\left( { - 2\pi ;2\pi } \right)\backslash \left\{ { - \pi ;0;\pi } \right\}\) là \(\left( { - 2\pi ; - \pi } \right),\left( { - \pi ,0} \right),\left( {0;\pi } \right),\left( {\pi ;2\pi } \right)\).