Giải mục 4 trang 66, 67 SGK Toán 9 tập 2 - Cùng khám phá — Không quảng cáo

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 66 SGK Toán 9 Cùng khám phá

Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:

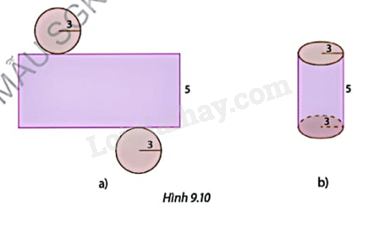
Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt (Hình 9.10a)

Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ (Hình 9.10b).

Phương pháp giải:

Đọc kĩ dữ liệu đề bài và thực hành theo.

Lời giải chi tiết:

LT4

Trả lời câu hỏi Luyện tập 4 trang 66 SGK Toán 9 Cùng khám phá

Tạo lập hình trụ có bán kính đáy 2,5 cm và chiều cao 4 cm.

Phương pháp giải:

Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:

Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt.

Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ.

Lời giải chi tiết:

HS tự thực hiện theo các bước trên.

VD3

Trả lời câu hỏi Vận dụng 3 trang 67 SGK Toán 9 Cùng khám phá

Tính diện tích xung quanh và thể tích của hình trụ có hình khai triển như Hình 9.11. Lấy \(\pi  \approx \frac{{22}}{7}\).

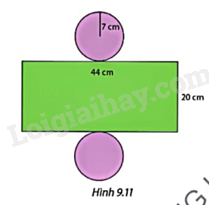
Phương pháp giải:

Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).

Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)

Lời giải chi tiết:

Diện tích xung quanh hình trụ là:

\({S_{xq}} = 2\pi rh = 2.\frac{{22}}{7}.7.20 = 880\) cm ² .

Thể tích hình trụ là:

V = \(\pi {r^2}h = \frac{{22}}{7}{.7^2}.20 = 3080\) cm ³ .