Giải mục 4 trang 35 SGK Toán 9 tập 1 - Cùng khám phá
a) Trong một mùa thi đấu giải vô địch bóng đá quốc gia, đội A ghi được ít bàn thắng hơn đội B, đội B lại ghi được ít bàn thắng hơn đội C. Gọi \(a,b,c\) lần lượt là số bàn thắng của đội A, B, C. Viết các bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\), giữa \(b\) và \(c\). b) Hình 2.2 cho biết biểu diễn của \(a\) trên trục số. Hãy biểu diễn \(b\) và \(c\) trên trục số. So sánh số bàn thắng của các đội A và C.
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 35 SGK Toán 9 Cùng khám phá
a) Trong một mùa thi đấu giải vô địch bóng đá quốc gia, đội A ghi được ít bàn thắng hơn đội B, đội B lại ghi được ít bàn thắng hơn đội C. Gọi \(a,b,c\) lần lượt là số bàn thắng của đội A, B, C. Viết các bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\), giữa \(b\) và \(c\).
b) Hình 2.2 cho biết biểu diễn của \(a\) trên trục số.
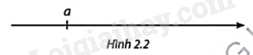
Hãy biểu diễn \(b\) và \(c\) trên trục số. So sánh số bàn thắng của các đội A và C.
Phương pháp giải:
Dựa vào định nghĩa bất đẳng thức để giải bài toán.
Lời giải chi tiết:
a) Bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\) là: \(a < b\).
Bất đẳng thức biểu thị quan hệ thứ tự giữa \(b\) và \(c\) là: \(b < c\).
b) Biểu diễn \(b\) và \(c\) trên trục số
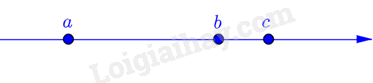
So sánh só bàn thắng của các đội A và C là: \(a < c\).
LT5
Trả lời câu hỏi Luyện tập 5 trang 35 S GK Toán 9 Cùng khám phá
Cho \(x \ge y\). Chứng minh rằng \(0,8x + 1 \ge 0,8y - 1\).
Phương pháp giải:
Dựa vào tính chất bắc cầu của thứ tự để giải bài toán.
Lời giải chi tiết:
Theo giả thiết thì \(x \ge y\). Nhân \(0,8\) vào hai vế của bất đẳng thức, ta có \(0,8x \ge 0,8y\). (1)
Cộng 1 vào hai vế của bất đẳng thức (1), ta được \(0,8x + 1 \ge 0,8y + 1\). (2)
Mặt khác, vì \(1 > - 1\) nên \(0,8y + 1 > 0,8y - 1\). (3)
Từ (2) và (3), sử dụng tính chất bắc cầu, suy ra \(0,8x + 1 \ge 0,8y - 1\).