Giải mục 3 trang 119, 120, 121 SGK Toán 9 tập 1 - Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1. Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 119 SGK Toán 9 Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
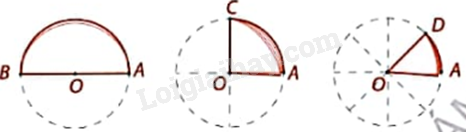
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Phương pháp giải:
+ Số đo các cung AB, AC, AD lần lượt có số đo là \({180^o}\), \({90^o}\), \({45^o}\).
+ Tỉ số của số đo cung và \({360^o}\) bằng thương giữa số đo cung tương ứng và \({360^o}\).
+ Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
Lời giải chi tiết:
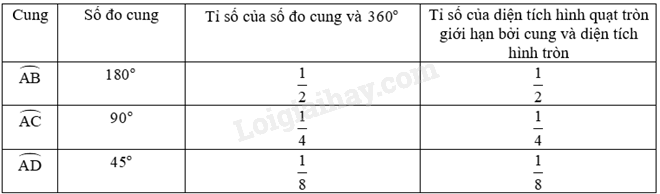
Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
LT3
Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\).
Phương pháp giải:
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\) là:
\({S_q} = \frac{{\pi {{.3}^2}.210}}{{360}} = \frac{{21\pi }}{4}\left( {c{m^2}} \right)\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm.
Phương pháp giải:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; R) và (O; r) (với \(r < R\)): \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\).
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm là:
\({S_{vk}} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {c{m^2}} \right)\).
VD
Trả lời câu hỏi Vận dụng trang 121 SGK Toán 9 Cùng khám phá
Trong Hình 5.54 , chiếc quạt có dạng một hình quạt tròn tâm O cung AB, bán kính \(OA = OB = 20cm\). Giấy được dán trong phần giới hạn bởi cung AB, cung CD, đoạn thẳng AC và BD với \(OC = OD = 10cm\). Biết khi mở rộng tối đa, hai nan quạt ngoài cùng tạo thành một góc \(\widehat {AOB} = {140^o}\). Tính chu vi và diện tích mảnh giấy để dán một mặt quạt (diện tích mép không đáng kể).

Phương pháp giải:
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Ta có: \(BD = AC = OB - OD = 20 - 10 = 10cm\).
Diện tích hình quạt tâm O, cung AB là:
\({S_{AOB}} = \frac{{\pi {{.20}^2}.140}}{{360}} = \frac{{1400}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích hình quạt tâm O, cung CD là:
\({S_{COD}} = \frac{{\pi {{.10}^2}.140}}{{360}} = \frac{{350}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích mảnh giấy để dán một mặt quạt là:
\(S = {S_{AOB}} - {S_{COD}} = \frac{{1400}}{9}\pi - \frac{{350}}{9}\pi = \frac{{350}}{3}\pi \left( {c{m^2}} \right)\).
Độ dài cung AB là:
\({l_{AB}} = \frac{{\pi .20.140}}{{180}} = \frac{{140}}{9}\pi \left( {cm} \right)\).
Độ dài cung CD là:
\({l_{CD}} = \frac{{\pi .10.140}}{{180}} = \frac{{70}}{9}\pi \left( {cm} \right)\).
Chu vi mảnh giấy để dán một mặt quạt là:
\(AC + BD + {l_{AB}} + {l_{CD}} = 10 + 10 + \frac{{140\pi }}{9} + \frac{{70\pi }}{9} = 20 + \frac{{70\pi }}{3}\left( {cm} \right)\)